
e
The Story of a Number
e
The Story of a Number
Eli Maor
PRINCETON UNIVERSITY PRESS
PRINCETON AND OXFORD
Copyright 1994 by Princeton University Press
Published by Princeton University Press,
41 William Street, Princeton, NJ 08540
In the United Kingdom: Princeton University Press,
6 Oxford Street, Woodstock, Oxfordshire OX20 1TW
press.princeton.edu
All Rights Reserved
First printing, 1994
New Princeton Science Library paperback printing, 2015
New Paperback ISBN: 978-0-691-16848-7
The Library of Congress cataloged the cloth edition of this book as follows:
Maor, Eli.
e : the story of a number / Eli Maor.
p. cm.
Includes bibliographical references and index.
ISBN 0-691-03390-0
1. e (The number) I. Title.
QA247.5.M33 1994
512'.73dc20 93-39003
British Library Cataloging-in-Publication Data is available
This book has been composed in Adobe Times Roman
Printed on acid-free paper.
Printed in the United States of America
1 3 5 7 9 10 8 6 4 2
I n memory of my parents, Richard and Luise Metzger
Philosophy is written in this grand bookI mean the universewhich stands continually open to our gaze, but it cannot be understood unless one first learns to comprehend the language and interpret the characters in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures, without which it is humanly impossible to understand a single word of it.
G ALILEO G ALILEI, Il Saggiatore (1623)
Contents
Preface
I t must have been at the age of nine or ten when I first encountered the number . My father had a friend who owned a workshop, and one day I was invited to visit the place. The room was filled with tools and machines, and a heavy oily smell hung over the place. Hardware had never particularly interested me, and the owner must have sensed my boredom when he took me aside to one of the bigger machines that had several flywheels attached to it. He explained that no matter how large or small a wheel is, there is always a fixed ratio between its circumference and its diameter, and this ratio is about 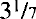 . I was intrigued by this strange number, and my amazement was heightened when my host added that no one had yet written this number exactlyone could only approximate it. Yet so important is this number that a special symbol has been given to it, the Greek letter . Why, I asked myself, would a shape as simple as a circle have such a strange number associated with it? Little did I know that the very same number had intrigued scientists for nearly four thousand years, and that some questions about it have not been answered even today.
. I was intrigued by this strange number, and my amazement was heightened when my host added that no one had yet written this number exactlyone could only approximate it. Yet so important is this number that a special symbol has been given to it, the Greek letter . Why, I asked myself, would a shape as simple as a circle have such a strange number associated with it? Little did I know that the very same number had intrigued scientists for nearly four thousand years, and that some questions about it have not been answered even today.
Several years later, as a high school junior studying algebra, I became intrigued by a second strange number. The study of logarithms was an important part of the curriculum, and in those dayswell before the appearance of hand-held calculatorsthe use of logarithmic tables was a must for anyone wishing to study higher mathematics. How dreaded were these tables, with their green cover, issued by the Israeli Ministry of Education! You got bored to death doing hundreds of drill exercises and hoping that you didnt skip a row or look up the wrong column. The logarithms we used were called commonthey used the base 10, quite naturally. But the tables also had a page called natural logarithms. When I inquired how anything can be more natural than logarithms to the base 10, my teacher answered that there is a special number, denoted by the letter e and approximately equal to 2.71828, that is used as a base in higher mathematics. Why this strange number? I had to wait until my senior year, when we took up the calculus, to find out.
In the meantime had a cousin of sorts, and a comparison between the two was inevitableall the more so since their values are so close. It took me a few more years of university studies to learn that the two cousins are indeed closely related and that their relationship is all the more mysterious by the presence of a third symbol, i, the celebrated imaginary unit, the square root of 1. So here were all the elements of a mathematical drama waiting to be told.
The story of has been extensively told, no doubt because its history goes back to ancient times, but also because much of it can be grasped without a knowledge of advanced mathematics. Perhaps no book did better than Petr Beckmanns A History of , a model of popular yet clear and precise exposition. The number e fared less well. Not only is it of more modern vintage, but its history is closely associated with the calculus, the subject that is traditionally regarded as the gate to higher mathematics. To the best of my knowledge, a book on the history of e comparable to Beckmanns has not yet appeared. I hope that the present book will fill this gap.
My goal is to tell the story of e on a level accessible to readers with only a modest background in mathematics. I have minimized the use of mathematics in the text itself, delegating several proofs and derivations to the appendixes. Also, I have allowed myself to digress from the main subject on occasion to explore some side issues of historical interest. These include biographical sketches of the many figures who played a role in the history of e, some of whom are rarely mentioned in textbooks. Above all, I want to show the great variety of phenomenafrom physics and biology to art and musicthat are related to the exponential function ex, making it a subject of interest in fields well beyond mathematics.
On several occasions I have departed from the traditional way that certain topics are presented in calculus textbooks. For example, in showing that the function y = ex is equal to its own derivative, most textbooks first derive the formula d(ln x)/dx = 1/x, a long process in itself. Only then, after invoking the rule for the derivative of the inverse function, is the desired result obtained. I have always felt that this is an unnecessarily long process: one can derive the formula d(ex)/dx = ex directlyand much fasterby showing that the derivative of the general exponential function y = bx is proportional to bx and then finding the value of b for which the proportionality constant is equal to 1 (this derivation is given in .
In the course of my research, one fact became immediately clear: the number e was known to mathematicians at least half a century before the invention of the calculus (it is already referred to in Edward Wrights English translation of John Napiers work on logarithms, published in 1618). How could this be? One possible explanation is that the number e first appeared in connection with the formula for compound interest. Someonewe dont know who or whenmust have noticed the curious fact that if a principal P is compounded n times a year for t years at an annual interest rate r, and if n is allowed to increase without bound, the amount of money S, as found from the formula S = P(1 + r/n)nt, seems to approach a certain limit. This limit, for P = 1, r = 1, and t = 1, is about 2.718. This discoverymost likely an experimental observation rather than the result of rigorous mathematical deductionmust have startled mathematicians of the early seventeenth century, to whom the limit concept was not yet known. Thus, the very origins of the the number
Next page











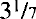 . I was intrigued by this strange number, and my amazement was heightened when my host added that no one had yet written this number exactlyone could only approximate it. Yet so important is this number that a special symbol has been given to it, the Greek letter . Why, I asked myself, would a shape as simple as a circle have such a strange number associated with it? Little did I know that the very same number had intrigued scientists for nearly four thousand years, and that some questions about it have not been answered even today.
. I was intrigued by this strange number, and my amazement was heightened when my host added that no one had yet written this number exactlyone could only approximate it. Yet so important is this number that a special symbol has been given to it, the Greek letter . Why, I asked myself, would a shape as simple as a circle have such a strange number associated with it? Little did I know that the very same number had intrigued scientists for nearly four thousand years, and that some questions about it have not been answered even today.