1.1 The Origins of Mathematical Logic
Logic formalizes valid methods of reasoning. The study of logic was begun by the ancient Greeks whose educational system stressed competence in reasoning and in the use of language. Along with rhetoric and grammar, logic formed part of the trivium , the first subjects taught to young people. Rules of logic were classified and named. The most widely known set of rules are the syllogisms ; here is an example of one form of syllogism:
Premise All rabbits have fur.
Premise Some pets are rabbits.
Conclusion Some pets have fur.
If both premises are true, the rules ensure that the conclusion is true.
Logic must be formalized because reasoning expressed in informal natural language can be flawed. A clever example is the following syllogism given by Smullyan (, p. 183):
Premise Some cars rattle.
Premise My car is some car.
Conclusion My car rattles.
The formalization of logic began in the nineteenth century as mathematicians attempted to clarify the foundations of mathematics. One trigger was the discovery of non-Euclidean geometries: replacing Euclids parallel axiom with another axiom resulted in a different theory of geometry that was just as consistent as that of Euclid. Logical systemsaxioms and rules of inferencewere developed with the understanding that different sets of axioms would lead to different theorems. The questions investigated included:
Consistency
A logical system is consistent if it is impossible to prove both a formula and its negation.
Independence
The axioms of a logical system are independent if no axiom can be proved from the others.
Soundness
All theorems that can be proved in the logical system are true.
Completeness
All true statements can be proved in the logical system.
Clearly, these questions will only make sense once we have formally defined the central concepts of truth and proof .
During the first half of the twentieth century, logic became a full-fledged topic of modern mathematics. The framework for research into the foundations of mathematics was called Hilberts program , (named after the great mathematician David Hilbert). His central goal was to prove that mathematics, starting with arithmetic, could be axiomatized in a system that was both consistent and complete. In 1931, Kurt Gdel showed that this goal cannot be achieved: any consistent axiomatic system for arithmetic is incomplete since it contains true statements that cannot be proved within the system.
In the second half of the twentieth century, mathematical logic was applied in computer science and has become one of its most important theoretical foundations. Problems in computer science have led to the development of many new systems of logic that did not exist before or that existed only at the margins of the classical systems. In the remainder of this chapter, we will give an overview of systems of logic relevant to computer science and sketch their applications.
1.2 Propositional Logic
Our first task is to formalize the concept of the truth of a statement. Every statement is assigned one of two values, conventionally called true and false or T and F . These should be considered as arbitrary symbols that could easily be replaced by any other pair of symbols like 1 and 0 or even and .
Our study of logic commences with the study of propositional logic (also called the propositional calculus ). The formulas of the logic are built from atomic propositions , which are statements that have no internal structure. Formulas can be combined using Boolean operators . These operators have conventional names derived from natural language ( and , or , implies ), but they are given a formal meaning in the logic. For example, the Boolean operator and is defined as the operator that gives the value true if and only if applied to two formulas whose values are true .
Example 1.1
The statements one plus one equals two and Earth is farther from the sun than Venus are both true statements; therefore, by definition, so is the following statement:
one plus one equals two and Earth is farther from the sun than Venus.
Since Earth is farther from the sun than Mars is a false statement, so is:
one plus one equals two and Earth is farther from the sun than Mars.
Rules of syntax define the legal structure of formulas in propositional logic. The semantics the meaning of formulasis defined by interpretations , which assign one of the (truth) values T or F to every atomic proposition. For every legal way that a formula can be constructed, a semantical rule specifies the truth value of the formula based upon the values of its constituents.
Proof is another syntactical concept. A proof is a deduction of a formula from a set of formulas called axioms using rules of inference . The central theoretical result that we prove is the soundness and completeness of the axiom system: the set of provable formulas is the same as the set of formulas which are always true.
Propositional logic is central to the design of computer hardware because hardware is usually designed with components having two voltage levels that are arbitrarily assigned the symbols 0 and 1. Circuits are described by idealized elements called logic gates ; for example, an and -gate produces the voltage level associated with 1 if and only if both its input terminals are held at this same voltage level.
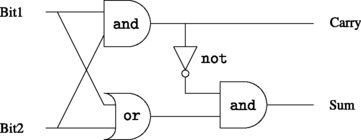
Example 1.2
Here is a half-adder constructed from and , or - and not -gates.
The half-adder adds two one-bit binary numbers and by joining several half-adders we can add binary numbers composed of many bits.
Propositional logic is widely used in software, too. The reason is that any program is a finite entity. Mathematicians may consider the natural numbers to be infinite (0,1,2,), but a word of a computers memory can only store numbers in a finite range. By using an atomic proposition for each bit of a programs state, the meaning of a computation can be expressed as a (very large) formula. Algorithms have been developed to study properties of computations by evaluating properties of formulas in propositional logic.
1.3 First-Order Logic
Propositional logic is not sufficiently expressive for formalizing mathematical theories such as arithmetic. An arithmetic expression such as x +2> y 1 is neither true nor false: (a) its truth depends on the values of the variables x and y ; (b) we need to formalize the meaning of the operators + and as functions that map a pair of numbers to a number; (c) relational operators like > must be formalized as mapping pairs of numbers into truth values. The system of logic that can be interpreted by values, functions and relations is called first-order logic (also called predicate logic or the predicate calculus ).