Shayle R. Searle - Linear Models

Linear Models

Copyright 1971 by John Wiley & Sons, Inc.

Wiley Classics Library Edition Published 1997

All rights reserved. Published simultaneously in Canada.

Reproduction or translation of any part of this work beyond that permitted by Sections 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful. Requests for permission or further information should be addressed to the Permissions Department, John Wiley & Sons, Inc., 605 Third Avenue, New York, NY 10158-0012.

Library of Congress Catalog Card Number: 70-138919

ISBN 0-471-18499-3

Preface

This book describes general procedures of estimation and hypothesis testing for linear statistical models and shows their application for unbalanced data (i.e., unequal-subclass-numbers data) to certain specific models that often arise in research and survey work. In addition, three chapters are devoted to methods and results for estimating variance components, particularly from unbalanced data. Balanced data of the kind usually arising from designed experiments are treated very briefly, as just special cases of unbalanced data. Emphasis on unbalanced data is the backbone of the book, designed to assist those whose data cannot satisfy the strictures of carefully managed and well-designed experiments.

The title may suggest that this is an all-embracing treatment of linear models. This is not the case, for there is no detailed discussion of designed experiments. Moreover, the title is not An Introduction to , because the book provides more than an introduction; nor is it with Applications, because, although concerned with applications of general linear model theory to specific models, few applications in the form of real-life data are used. Similarly, for Unbalanced Data has also been excluded from the title because the book is not devoted exclusively to such data. Consequently the title Linear Models remains, and I believe it has brevity to recommend it.

My main objective is to describe linear model techniques for analyzing unbalanced data. In this sense the book is self-contained, based on prerequisites of a semester of matrix algebra and a year of statistical methods. The matrix algebra required is supplemented in Chapter 1, which deals with generalized inverse matrices and allied topics. The reader who wishes to pursue the mathematics in detail throughout the book should also have some knowledge of statistical theory. The requirements in this regard are supplemented by a summary review of distributions in Chapter 2, extending to sections on the distribution of quadratic and bilinear forms and the singular multinormal distribution. There is no attempt to make this introductory material complete. It serves to provide the reader with foundations for developing results for the general linear model, and much of the detail of this and other chapters can be omitted by the reader whose training in mathematical statistics is sparse. However, he must know Theorems 1 through 3 of Chapter 2, for they are used extensively in succeeding chapters.

Chapter 3 deals with full-rank models. It begins with a simple explanation of regression (based on an example) and proceeds to multiple regression, giving a unified treatment for testing a general linear hypothesis. After dealing with various aspects of this hypothesis and special cases of it, the chapter ends with sections on reduced models and other related topics. Chapter 4 introduces models not of full rank by discussing regression on dummy (0, 1) variables and showing its equivalence to linear models. The results are well known to most statisticians, but not to many users of regression, especially those who are familiar with regression more in the form of computer output than as a statistical procedure. The chapter ends with a numerical example illustrating both the possibility of having many solutions to normal equations and the idea of estimable and non-estimable functions.

Chapter 5 deals with the non-full-rank model, utilizing generalized inverse matrices and giving a unified procedure for testing any testable linear hypothesis. Chapters 6 through 8 deal with specific cases of this model, giving many details for the analysis of unbalanced data. Within these chapters there is detailed discussion of certain topics that other books tend to ignore: restrictions on models and constraints on solutions (Sections 5.6 and 5.7); singular covariance matrices of the error terms (Section 5.8); orthogonal contrasts with unbalanced data (Section 5.5g); the hypotheses tested by F-statistics in the analysis of variance of unbalanced data (Sections 6.4f, 7.1g, and 7.2f); analysis of covariance for unbalanced data (Section 8.2); and approximate analyses for data that are only slightly unbalanced (Section 8.3). On these and other topics, I have tried to coordinate some ideas and make them readily accessible to students, rather than continuing to leave the literature relatively devoid of these topics or, at best, containing only scattered references to them. Statisticians concerned with analyzing unbalanced data on the basis of linear models have talked about the difficulties involved for many years but, probably because: the problems are not easily resolved, little has been put in print about them. The time has arrived, I feel, for trying to fill this void. Readers may not always agree with what is said, indeed I may want to alter some things myself in due time but, meanwhile, if this book sets readers to thinking and writing further about these matters, I will feel justified. For example, there may be criticism of the discussion of F-statistics in parts of Chapters 6 through 8, where these statistics are used, not so much to test hypotheses of interest (as described in Chapter 5), but to specify what hypotheses are being tested by those F-statistics available in analysis of variance tables for unbalanced data. I believe it is important to understand what these hypotheses are, because they are not obvious analogs of the corresponding balanced data hypotheses and, in many cases, are relatively useless.

The many numerical illustrations and exercises in Chapters 3 through 8 use hypothetical data, designed with easy arithmetic in mind. This is because I agree with C. C. Li (1964) who points out that we do not learn to solve quadratic equations by working with something like

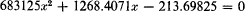
just because it occurs in real life. Learning to first solve x2 + 3x + 2 = 0 is far more instructive. Whereas real-life examples are certainly motivating, they usually involve arithmetic that becomes as cumbersome and as difficult to follow as is the algebra it is meant to illustrate. Furthermore, if one is going to use real-life examples, they must come from a variety of sources in order to appeal to a wide audience, but the changing from one example to another as succeeding points of analysis are developed and illustrated brings an inevitable loss of continuity. No apology is made, therefore, for the artificiality of the numerical examples used, nor for repeated use of the same example in many places. The attributes of continuity and of relatively easy arithmetic more than compensate for the lack of reality by assuring that examples achieve their purpose, of illustrating the algebra.

Chapters 9 through 11 deal with variance components. The first part of Chapter 9 describes random models, distinguishing them from fixed models by a series of examples and using the concepts, rather than the details, of the examples to make the distinction. The second part of the chapter is the only occasion where balanced data are discussed in depth: not for specific models (designs) but in terms of procedures applicable to balanced data generally. Chapter 10 presents methods currently available for estimating variance components from unbalanced data, their properties, procedures, and difficulties. Parts of these two chapters draw heavily on Searle (1971). Finally, Chapter 11 catalogs results derived by applying to specific models some of the methods described in Chapter 10, gathering together the cumbersome algebraic expressions for variance component estimators and their variances in the 1-way, 2-way nested, and 2-way crossed classifications (random and mixed models), and others. Currently these results are scattered throughout the literature. The algebraic expressions are themselves so lengthy that there would be little advantage in giving numerical illustrations. Instead, extra space has been taken to typeset the algebraic expressions in as readable a manner as possible.