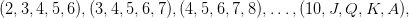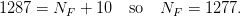Solutions to the Questions in
An Introduction to Mathematical Statistics
and Its Applications
by Richard J. Larsen and Morris L. Marx
John Weatherwax
Text copyright 2018 John L. Weatherwax
All Rights Reserved
Please Do Not Redistribute Without Permission from the Author
To my family.
Introduction
This is a solution manual all of the questions in the excellent statistical textbook:
An Introduction to Mathematical Statistics and Its Applications
by Richard Larsen and Morris Marx
This solution manual was prepared form the fifth edition of the textbook. I have looked at other editions of the book and have had a hard time finding any significant differences between the editions.
Ive tried to provide much more detail than is normally found in a typical solutions manual. Thus rather than just give the solution I try to explain in great detail how I arrived a the solution. This will further reinforce the main ideas from class and better teach the material. The manual stands at over 400 pages.
One of the benefits of this manual is that I heavily use the R statistical language to perform any of the needed numerical computations (rather than do them by-hand). Thus if you use this manual you will be learning some R programming at the same time as you learn statistics. The R programming language is one of the most desired skills for anyone who hopes to use data/statistics in their future career. All the R code can be found at the following location:
http://waxworksmath.com/Authors/G_M/Larsen/larsen.html
As a final comment, Ive worked hard to make these notes as good as I can, but I have no illusions that they are perfect. If you feel that that there is a better way to accomplish or explain an exercise or derivation presented in these notes; or that one or more of the explanations is unclear, incomplete, or misleading, please tell me. If you find an error of any kind technical, grammatical, typographical, whatever please tell me that, too. Ill gladly add to the acknowledgments in later printings the name of the first person to bring each problem to my attention.
Chapter 2 (Probability)
In working some of these questions I have chosen to use R or python to explicitly enumerate the spaces requested rather than to derive them by hand. While many of these questions could no doubt be done by hand it is very easy to change a problem statement in such a way that will make that impossible. Using a computer is a more robust (with respect to problem specification) way to work problems like these and is a helpful skill to have.
Question 2.2.1
The full sample space in this case would be
Event A would be the set
Event B would be the set
Question 2.2.2
We can use R to enumerate the possible outcomes when we toss three die. We have
D = 1:6
outcomes = expand.grid(D, D, D)
colnames(outcomes) = c(R, B, G)
mask = apply(outcomes, 1, sum) == 5
print(outcomes[mask, ])
Running the above we get
> print(outcomes[mask, ])
R B G
3 3 1 1
8 2 2 1
13 1 3 1
38 2 1 2
43 1 2 2
73 1 1 3
for the members of the event A .
Question 2.2.3
We can generate this sample space with the following python code
from itertools import combinations
for it in combinations(range(1, 7), 3):
if sorted(it)[1]==3: print it
Running the above python code gives
(1, 3, 4)
(1, 3, 5)
(1, 3, 6)
(2, 3, 4)
(2, 3, 5)
(2, 3, 6)
for the elements of the sample space.
Question 2.2.4
We can pick the suit of the first card in four ways. We can pick the number on the first card to be one of the numbers 1 , 2 , 3 , 4 , 5 , 6 , 7. For all of these choices (excluding 4) the number on the other card required that the two cards sum to 8 is determined and different than the number on the first card. Ignoring the choice of the number 4 (for the time being) on the first card we have 7 1 = 6 ways to pick the number. We then have four ways to pick the suit of the second card. This gives
total ways to draw this type of pair.
If we pick the number 4 on the first card the number 4 must be picked on the second card (so the sum is eight) and we thus cant select the same suit for the second card as we did on the first card. This means that the number of ways we can draw two cards that sum two eight in this way is
The total number of ways to pick this type of pairs is the sum of the two above numbers or 96 + 12 = 108.
Question 2.2.5
One would expect that this would have the sum of the two die to be eight and is perhaps the special case where both die show four.
Question 2.2.6
There are 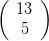 = 1287 ways to draw five cards in the suit of hearts (i.e. a flush). The straight flushes are
= 1287 ways to draw five cards in the suit of hearts (i.e. a flush). The straight flushes are
of which there are ten such hands. If we let N F be the number of flushes of the form we are interested in then
Question 2.2.7
This would be the set of triangles that satisfy a + b = 5 .
Question 2.2.8
We can generate this sample space using the following python code
from itertools import permutations
for it in permutations(B B B S S.split(), 5):
print it
Running the above give the following output (partial)
(B, B, B, S, S)
(B, B, B, S, S)
(B, B, S, B, S)
(B, B, S, S, B)
(B, B, S, B, S)
(B, B, S, S, B)
Question 2.2.9
Part (a): We can generate this sample space using the following R code
R = 0:1
outcomes = expand.grid(R, R, R, R)
colnames(outcomes) = c(P1, P2, P3, P4)
Running the above give the following output (partial)
> outcomes
P1 P2 P3 P4
1 0 0 0 0
2 1 0 0 0
3 0 1 0 0
4 1 1 0 0
5 0 0 1 0
6 1 0 1 0
Part (b): To find the events where exactly two phones were used we could do
mask = apply(outcomes, 1, sum) == 2
outcomes[mask, ]
which gives
> outcomes[mask, ]
P1 P2 P3 P4
4 1 1 0 0
6 1 0 1 0
7 0 1 1 0
10 1 0 0 1
11 0 1 0 1
13 0 0 1 1
Part (c): We will have at most space for one more call if there is only one unused phone (or no unused phones). As the one free phone can be in any of the k spaces we have k outcomes. The stated event will also occur if all the phones are in use which can happen in only one way. The the total number of outcomes for this event is k + 1.











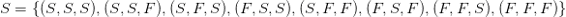
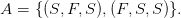
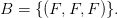
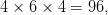
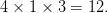
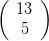 = 1287 ways to draw five cards in the suit of hearts (i.e. a flush). The straight flushes are
= 1287 ways to draw five cards in the suit of hearts (i.e. a flush). The straight flushes are