Contents
Pagebreaks of the print version

CORRECT ANTIDIFFERENTIATION
The Change of Variable Well Done
CORRECT ANTIDIFFERENTIATION
The Change of Variable Well Done
Antonio Martnez-AbejnUniversity of Oviedo, Spain Published by
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224
USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601
UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE
Library of Congress Cataloging-in-Publication Data Names: Martinez-Abejon, Antonio, author. Title: Correct antidifferentiation : the change of variable well done / Antonio Martinez-Abejon, University of Oviedo, Spain. Description: New Jersey : World Scientific, [2021] | Includes bibliographical references and index.
Identifiers: LCCN 2020040370 | ISBN 9789811227455 (hardcover) | ISBN 9789811227462 (ebook for institutions) | ISBN 9789811227479 (ebook for individuals) Subjects: LCSH: Functions of real variables. Classification: LCC QA331.5 .M286 2021 | DDC 515/.8--dc23 LC record available at https://lccn.loc.gov/2020040370 British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. Copyright 2021 by World Scientific Publishing Co. Pte. Ltd. All rights reserved.
This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher. For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher. For any available supplementary material, please visit
https://www.worldscientific.com/worldscibooks/10.1142/12021#t=suppl Printed in Singapore To my son Robert
Preface
This book is primarily concerned with the correct calculation of antiderivatives of elementary real-valued functions of a real variable and the correct understanding of these calculations, with particular emphasis on the technique of change of variable. The motivation for this book is that, in my opinion, most of the circulating materials do not treat the subject of antidifferentiation with sufficient strength or generality. Indeed, when an antiderivative of a given function
f(
x) is needed and a change of variable
x =
g(
t) is available, the substitution formulas
x =
g(
t) and
dx =
g(
t)
dt transform the expression
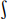 f
f(
x)
dx into
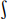
(
fg)(
t)
g(
t)
dt, and if an antiderivative
H(
t) of (
fg)(
t)
g(
t) is known, the function
F(
x) :=
Hg1(
x) is usually claimed to be an antiderivative of
f(
x).
But this is only partially true. In fact, there are standard cases where F coincides with f but locally, that is, F(x) = f(x) for xA where A is a certain subset properly contained in the domain of f, whereas F(x) is not even continuous at the points xA, or f is differentiable at xA but F(x) 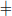 f(x). That means some modifications still need to be made on F(x) to manage an antiderivative F(x) of f(x) on the entire domain of f. Notice that most software packages for Symbolic Calculus stop at the local antiderivative F(x) as a definitive solution for
f(x). That means some modifications still need to be made on F(x) to manage an antiderivative F(x) of f(x) on the entire domain of f. Notice that most software packages for Symbolic Calculus stop at the local antiderivative F(x) as a definitive solution for 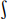 f(x) dx, so they reach a correct solution only when, by chance, F(x) = F(x) for all x. Undergraduate texts, which have to treat a lot of topics in a short space, deal only with those functions f(x) for which the identity F(x) = F(x) holds; but they do not generally discuss how to know whether or not F(x) is a true antiderivative of f(x) and, eventually, this is misleading. Higher level books usually refer all issues about elementary antidifferentiation back to undergraduate texts.
f(x) dx, so they reach a correct solution only when, by chance, F(x) = F(x) for all x. Undergraduate texts, which have to treat a lot of topics in a short space, deal only with those functions f(x) for which the identity F(x) = F(x) holds; but they do not generally discuss how to know whether or not F(x) is a true antiderivative of f(x) and, eventually, this is misleading. Higher level books usually refer all issues about elementary antidifferentiation back to undergraduate texts.
This book fills the gap by explaining how to reshape F(x) to obtain a true antiderivative F(x) of f(x). Let us insist on the fact that the process of passing from F(x) to F(x) cannot be done by means of an algorithm, so it must be learnt by example. However, all actions required for this process are simple and fit perfectly into an undergraduate programme. It is worth pointing out that the interest of Real Mathematical Analysis in Antidifferentiation has evolved towards very sophisticated theories on the existence of antiderivatives for certain classes of functions ([Bruckner (1978)], [Ciesielski et Seoane (2018)], [Petruska (1974)]), while every theoretical or practical aspect concerning the calculation of antiderivatives has moved into Computational Algebra as witnessed by the software derived from the Risch algorithm [Risch (1969)], [Risch (1970)] (see also [Bronstein (1997)]). In a certain sense, this book is saying that Real Mathematical Analysis still has a say in the calculation of antiderivatives. This book is organized into three parts.
Part 1 goes from and the appendices. These appendices cover those aspects that do not fit well in Parts 1 or 2 but that are still necessary to make this book reasonably self-contained. Since this book is oriented to the practice of antidifferentiation, Part 1 does not include a list of examples or exercises. Indeed, most calculus handbooks do an excellent job in that, so we cannot offer any improvement. However, each chapter of the Part 2 contains plenty of examples along with a list of exercises and solutions. consists of a quick survey on real numbers, limit points of sets, limits of real sequences and compactness in the real line. are developed by means of sequential characterizations, which reduce the multiplicity of cases and, in my opinion, are more intuitive than the typical - arguments. are developed by means of sequential characterizations, which reduce the multiplicity of cases and, in my opinion, are more intuitive than the typical - arguments.
Matters like convexity, extrema of functions and such have been omitted since they are not relevant in antidifferentiation. A theory of integration is needed to manage results of existence of antiderivatives for continuous functions on intervals. Probably the best integral for this purpose is that of HenstockKurzweil, but our choice is the integral of Riemann since it is simpler and is perfectly adapted to the scope of this book. introduces the fundamental functions from the core of elementary antidifferentiation: polynomials, n-th roots, the exponential function, the natural logarithm, the circular functions and the hyperbolic functions. The functions log x, ex, cos x and sin












 Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE Library of Congress Cataloging-in-Publication Data Names: Martinez-Abejon, Antonio, author. Title: Correct antidifferentiation : the change of variable well done / Antonio Martinez-Abejon, University of Oviedo, Spain. Description: New Jersey : World Scientific, [2021] | Includes bibliographical references and index.
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE Library of Congress Cataloging-in-Publication Data Names: Martinez-Abejon, Antonio, author. Title: Correct antidifferentiation : the change of variable well done / Antonio Martinez-Abejon, University of Oviedo, Spain. Description: New Jersey : World Scientific, [2021] | Includes bibliographical references and index. 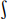 f(x) dx into
f(x) dx into 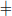 f(x). That means some modifications still need to be made on F(x) to manage an antiderivative F(x) of f(x) on the entire domain of f. Notice that most software packages for Symbolic Calculus stop at the local antiderivative F(x) as a definitive solution for
f(x). That means some modifications still need to be made on F(x) to manage an antiderivative F(x) of f(x) on the entire domain of f. Notice that most software packages for Symbolic Calculus stop at the local antiderivative F(x) as a definitive solution for