Jessica Wynne - Do Not Erase: Mathematicians and Their Chalkboards

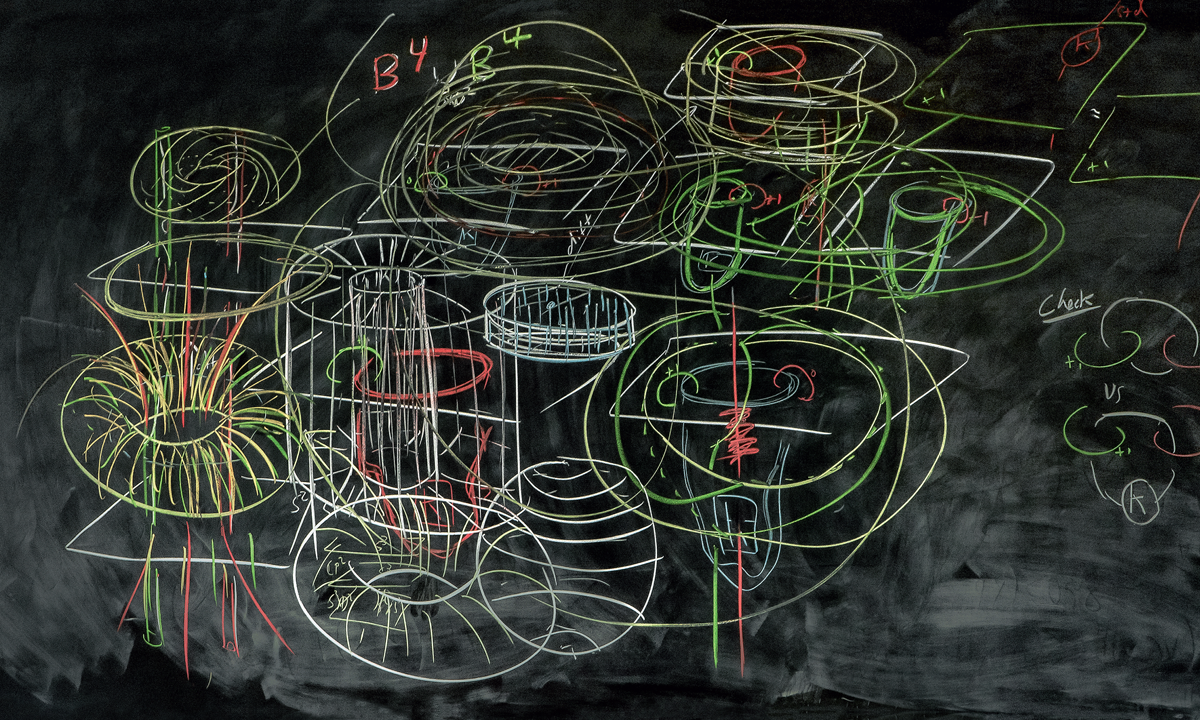
A PHOTOGRAPHIC EXPLORATION OF MATHEMATICIANS CHALKBOARDS

A mathematician, like a painter or poet, is a maker of patterns, wrote the British mathematician G. H. Hardy. In Do Not Erase, photographer Jessica Wynne presents remarkable examples of this idea through images of mathematicians chalkboards. While other fields have replaced chalkboards with whiteboards and digital presentations, mathematicians remain loyal to chalk for puzzling out their ideas and communicating their research. Wynne offers more than one hundred stunning photographs of these chalkboards, gathered from a diverse group of mathematicians around the world. The photographs are accompanied by essays from each mathematician, reflecting on their work and processes. Together, pictures and words provide an illuminating meditation on the unique relationships among mathematics, art, and creativity.

The mathematicians featured in this collection comprise exciting new voices alongside established figures, including Sun-Yung Alice Chang, Alain Connes, Misha Gromov, Andre Neves, Kasso Okoudjou, Peter Shor, Christina Sormani, Terence Tao, Claire Voisin, and many others. The companion essays give insights into how the chalkboard serves as a special medium for mathematical expression. The volume also includes an introduction by the author, an afterword by New Yorker writer Alec Wilkinson, and biographical information for each contributor.

Do Not Erase is a testament to the myriad ways that mathematicians use their chalkboards to reveal the conceptual and visual beauty of their disciplineshapes, figures, formulas, and conjectures created through imagination, argument, and speculation.

DO NOT ERASE

DO NOT ERASE

MATHEMATICIANS AND THEIR CHALKBOARDS

JESSICA WYNNE

AFTERWORD BY ALEC WILKINSON PRINCETON UNIVERSITY PRESS PRINCETON AND OXFORD

For my daughter, Molly

INTRODUCTION

I grew up in a house on the campus of a boarding school in Connecticut. My parents were teachers theremy mother taught art and my father taught history and coached the wrestling team. My life was immersed in this insular worldthe school was my home and my playground. On the weekends my sisters and I would play in the classrooms, the rooms were often hot and musty and smelled of teenagers and chalk.

Many years later, I find myself back in dusty, chalk-filled classrooms, photographing the chalkboards of eminent mathematicians. How did I get here? The deeper answer, most likely, is that it still feels like home to me. The more immediate reason, however, comes out of a conversation I had in another part of New England.

Every summer, I take a break from academia and leave my home in New York City to join my family in a small beach town on the outer tip of Cape Cod, Massachusetts. Over the years, Ive become very close to my neighbors, who live in a house once occupied by my paternal grandfather. Amie Wilkinson and Benson Farb are a married couple and parents of two. They are also theoretical mathematicians who teach at the University of Chicago. Amies research focuses on smooth dynamical systems and ergodic theory; Bensons work explores low-dimensional topology and geometric group theory.

Amie and Benson are theoretical or pure mathematicians, which means they do math for maths sake. They are interested in ideas, abstraction, exploring the boundaries of pure reason without explicit or immediate application in the physical worldakin to art, philosophy, poetry, and music. Practitioners of applied math, on the other hand, use theories and techniques to solve practical problems in the physical world. Although their objectives are different, these two branches of mathematics are inextricably linked: there are numerous examples of discoveries in pure math that would be revealed to have revolutionary applications years later. In fact, one could say that all modern technology is derived from pure mathematics.

One day on the Cape, I watch Benson work at his dining room table. He is listening to Indian ragas with the volume so loud I can hear the thumping beats of the tabla through his headphones. For several hours, he sits, thinking, creating, jotting down the occasional note. It looks like he has a secret. I feel like he is creating something so expansive and beautiful it is beyond words, something that exists only in his head.

When I ask him to explain what he is working on, he pauses, appears to struggle for the right words, and replies, simply, No. I cant.

Later, after giving it some thought, he tells me he is working on configuration spaces, thinking about all of the possible configurations of, say, 10,000 distinct points moving around in a 4-dimensional space. Benson notes that this is a 40,000-dimensional problem. Hes trying to discover patterns within this extremely complex system. Or in his more technical terms: Im trying to decompose the cohomology of the space of configurations of n points on a manifold as a direct sum of irreducible representations of the symmetric group S_n, where n can be any number (like 10,000).

Mathematics at Bensons level is not easily translatable to the layperson. Some things are just complicated and cannot be reduced in a meaningful way to a concise, easy-to-understand statement. It is like a special foreign language, unknowable to all but a few.

I have always used my camera as a way to understand and explore the world. At sixteen, I left my home in the Northeast to spend a year at a boarding school on a hill station in southern India. (My mother had attended the same school.)

Before I left, my father gave me a gift: a twin-lens reflex camera, medium format, heavy, clunky, with a beautifully worn brown leather strap and case. I loved it. I brought it with me to India and soon discovered that the camera is a powerful toolit made me feel fearless and allowed me to connect to people and places that were seemingly inaccessible. This was exciting to me.

Thirty years later, I return to India, this time leading a group of my photography students on a study abroad trip. We are in Jaipur, Rajasthan. I arrange a visit to an elementary school so my students can take portraits of the children, and the children can practice their English with us. The principal takes us through a maze of back doors and staircases to the roof of the schoolhouse. We emerge to discover that there are chalkboards surrounding the perimeter. Some are on stands; some are on the ground leaning against a low wall. All are filled with lessons in Hindi, a language that is foreign to me. The boards are beautiful but inaccessible. I walk around the roof and photograph each one.

Back home, as I sort through my photographs from the trip, I keep coming back to the images of the chalkboards. They symbolize so much for me: the interplay of aesthetic beauty and practical use; the foreign and the familiar; understanding and mystery. The writing on the boards in Jaipur reminds me of the mathematical symbols in Bensons notebook. I see this connection and the project begins to take shape.

The chalkboard is one of the oldest and most important analog tools for learning. At first, students used small, individual pieces of slate and would sit at their desks working on their boards. But their teachers had no way to share and demonstrate their work with an entire class. Although there is some dispute about the date, many believe that the first large chalkboard was installed in a classroom in 1801. Eventually it evolved into what we know now: a large object, typically with a black or green surface, hanging on a wall. No longer made of slate, most boards are made out of porcelain-enameled steel.