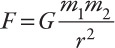John M. Henshaw - An Equation for Every Occasion: Fifty-Two Formulas and Why They Matter

An Equation for Every Occasion

Fifty-Two Formulas
and Why They Matter

John M. Henshaw

With contributions from Steven Lewis

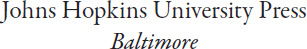
2014 Johns Hopkins University Press

All rights reserved. Published 2014

Printed in the United States of America on acid-free paper

2 4 6 8 9 7 5 3 1

Johns Hopkins University Press

2715 North Charles Street

Baltimore, Maryland 21218-4363

www.press.jhu.edu

Library of Congress Cataloging-in-Publication Data

Henshaw, John M., author.

An equation for every occasion : fifty-two formulas and why they matter / by John M. Henshaw ; with contributions from Steven Lewis.

pages cm

Includes bibliographical references and index.

ISBN-13: 978-1-4214-1491-1 (hardcover : alk. paper)

ISBN-10: 1-4214-1491-0 (hardcover : alk. paper)

ISBN-13: 978-1-4214-1492-8 (electronic)

ISBN-10: 1-4214-1492-9 (electronic)

1. Mathematical analysis. 2. Mathematical modelsMiscellanea. I. Title.

QA401.H457 2014

510dc23 2013050140

A catalog record for this book is available from the British Library.

Special discounts are available for bulk purchases of this book. For more information, please contact Special Sales at 410-516-6936 or .

Johns Hopkins University Press uses environmentally friendly book materials, including recycled text paper that is composed of at least 30 percent post-consumer waste, whenever possible.

To my students at the University of Tulsa

This is not a math book. Its a storybook. Its a book of fifty-two true stories, and as it happens, each one of those stories was inspired by a mathematical equation. Behind every equation lies a storysometimes many stories. And behind many stories, there lies an equationsometimes more than one. Our goal was to find those stories, and those equations, and to tell them as well as we could.

As a result, we are unable to avail ourselves of the sage advice given to the incomparable Stephen Hawking when he wrote the classic A Brief History of Time. In the acknowledgments to that book, Hawking notes that he had been warned that each equation he included in his book would halve the books sales. He thus decided to include only one such potential revenue reducer, Einsteins famous equation,

E = mc2.

While our book is also written for a general audience, its purpose is to present a new equation at the beginning of every chapter. It is thus our fervent hope that sales of this book do not adhere to the relationship suggested by Professor Hawkings advisor, presented here in the form of an equation:

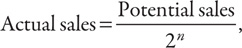
where n is the number of equations in the book.

There comes a point in the education of many children, particularly if they like math, when they realize that math is not just another subject to be studied and compartmentalized along with all the others. Often, it is in the early teenage years that many kids begin to realize that math is an indispensable tool for explaining the how and the why of so many things. A little bit later, those same teens begin to discover that math is good for something else, and that is for making the world a better place. Somewhere along the way it occurred to us that math has yet another purpose, and that is in storytelling. The stories in this book come from the worlds of science and engineering, but also from the worlds of business, the arts, and recreation. A good equation, like a good story, is where you find it.

In How to Read a Book, Mortimer J. Adler and Charles Van Doren offer sound advice on many things, including reading books that are liberally sprinkled with equations. They suggest, in part, that skipping is often the better part of valor. We agree. We hope that you will skip around lots as you read this book. The stories are shortone thousand words each, give or takeand they can be read in any order that you desire. Many, if not most, of the equations we write about merit longer treatment. Entire booksin some cases, shelves full of bookshave been written about some of them. That is not our purpose here. If, having read our book, you find yourself wanting more, we hope you will seek out some of the references we have provided for each story.

A mathematician, according to Lord Kelvin, is someone to whom the fact that the integral, from minus infinity to infinity, of ex2dx is equal to the square root of pi is as obvious as it is to you and to us that two plus two equals four. In equation form:

Lord Kelvin was right about most things (with a few famous exceptions), and we suspect his definition of a mathematician is not far from the mark. We hasten to add that we wrote this book for those of us in the latter (two plus two equals four) crowd. To the extent that those few members of the former (square root of pi) group find it an interesting read as well, we shall be grateful.

This book had its origins in an innocent little conversation I had with one of my students a few years ago. That was the day that Steven Lewis stopped by my office to see if I might be interested in pursuing an independent study project with him. Arent you the guy who is double majoring in mechanical engineering and English literature? I asked. He replied that this was indeed the case. Well, then, maybe we should write a book together! Although my offer was made somewhat in jest, it was eagerly accepted. And so, each week for the rest of the semester, we wrote one equation story apiece. During our weekly meetings we read our stories to each other and critiqued and discussed each others work. It was certainly the most unusual, and one of the most enjoyable, independent study projects Ive ever pursued. Steven eventually graduated and began his career as an engineer. And so it fell to me to round out the number of stories to fifty-two, do some editing, and wrap things up. But I shall always be grateful that Steven, with an undergraduates optimism, was so willing and able to help me get this project off the ground.

An Equation for Every Occasion

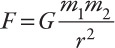
Newtons Law of Universal Gravitation

Newtons law of universal gravitation, which appears in Isaac Newtons Principia and was first published in 1687, states that the force, F, acting between two bodies of masses m1 and m2, is directly proportional to the product of the masses (m1m2) and inversely proportional to the square of the distance, r, between the bodies. In a consideration of the gravitational force of a large body such as a planet, the mass of the planet is taken to be concentrated at a single point at the very center of the planet. The gravitational effects of a spherically symmetric mass distribution, in regions exterior to it, is indistinguishable from that of a point mass at the center of the sphere. G is the universal gravitational constant, which is approximately 6.67 1011 m3 / (kg s2).