Claude E Shannon - The Mathematical Theory of Communication

1. The Discrete Noiseless Channel

Teletype and telegraphy are two simple examples of a discrete channel for transmitting information. Generally, a discrete channel will mean a system whereby a sequence of choices from a finite set of elementary symbols S1Sn can be transmitted from one point to another. Each of the symbols Si is assumed to have a certain duration in time ti seconds (not necessarily the same for different Si, for example the dots and dashes in telegraphy). It is not required that all possible sequences of the Si be capable of transmission on the system; certain sequences only may be allowed. These will be possible signals for the channel. Thus in telegraphy suppose the symbols are: (1) A dot, consisting of line closure for a unit of time and then line open for a unit of time; (2) A dash, consisting of three time units of closure and one unit open; (3) A letter space consisting of, say, three units of line open; (4) A word space of six units of line open. We might place the restriction on allowable sequences that no spaces follow each other (for if two letter spaces are adjacent, they are identical with a word space). The question we now consider is how one can measure the capacity of such a channel to transmit information.

In the teletype case where all symbols are of the same duration, and any sequence of the 32 symbols is allowed, the answer is easy. Each symbol represents five bits of information. If the system transmits n symbols per second it is natural to say that the channel has a capacity of 5n bits per second. This does not mean that the teletype channel will always be transmitting information at this ratethis is the maximum possible rate and whether or not the actual rate reaches this maximum depends on the source of information which feeds the channel, as will appear later.

In the more general case with different lengths of symbols and constraints on the allowed sequences, we make the following definition: The capacity C of a discrete channel is given by

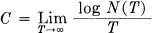
where N(T) is the number of allowed signals of duration T.

It is easily seen that in the teletype case this reduces to the previous result. It can be shown that the limit in question will exist as a finite number in most cases of interest. Suppose all sequences of the symbols S1,, Sn are allowed and these symbols have durations t1,, tn. What is the channel capacity? If N(t) represents the number of sequences of duration t we have

N(t) = N(tt1) + N(tt2) ++ N(ttn).

The total number is equal to the sum of the numbers of sequences ending in S1, S2,, Sn and these are N(tt1), N(tt2),, N(ttn), respectively. According to a well-known result in finite differences, N(t) is then asymptotic for large t to AX0 where A is constant and X0 is the largest real solution of the characteristic equation:

Xt1 + Xt2 ++ Xtn = 1

and therefore

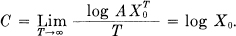
In case there are restrictions on allowed sequences we may still often obtain a difference equation of this type and find C from the characteristic equation. In the telegraphy case mentioned above

N(t) = N(t 2) + N(t 4) + N(t 5) + N(t 7)

+ N(t 8) + N(t 10)

as we see by counting sequences of symbols according to the last or next to the last symbol occurring. Hence C islog 0 where 0 is the positive root of 1 = 2 + 4 + 5 + 7 + 8 + 10. Solving this we find C = 0.539.

A very general type of restriction which may be placed on allowed sequences is the following: We imagine a number of possible states al, a2,, am. For each state only certain symbols from the set S1,, Sn can be transmitted (different subsets for the different states). When one of these has been transmitted the state changes to a new state depending both on the old state and the particular symbol transmitted. The telegraph case is a simple example of this. There are two states depending on whether or not a space was the last symbol transmitted. If so, then only a dot or a dash can be sent next and the state always changes. If not, any symbol can be transmitted and the state changes if a space is sent, otherwise it remains the same. The conditions can be indicated in a linear graph as shown in it is shown that if the conditions on allowed sequences can be described in this form C will exist and can be calculated in accordance with the following result:

Theorem 1: Let 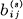be the duration of the sthsymbol which is allowable in state i and leads to stage j. Then the channel capacity C is equal to log W where W is the largest real root of the determinantal equation:

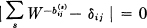
where ij = 1 if i = j and is zero otherwise.

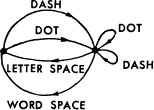
Fig. 2.Graphical representation of the constraints on telegraph symbols.

For example, in the telegraph case () the determinant is:

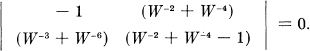
On expansion this leads to the equation given above for this set of constraints.

2. The Discrete Source of Information

We have seen that under very general conditions the logarithm of the number of possible signals in a discrete channel increases linearly with time. The capacity to transmit information can be specified by giving this rate of increase, the number of bits per second required to specify the particular signal used.

We now consider the information source. How is an information source to be described mathematically, and how much information in bits per second is produced in a given source? The main point at issue is the effect of statistical knowledge about the source in reducing the required capacity of the channel, by the use of proper encoding of the information. In telegraphy, for example, the messages to be transmitted consist of sequences of letters. These sequences, however, are not completely random. In general, they form sentences and have the statistical structure of, say, English. The letter E occurs more frequently than Q, the sequence TH more frequently than XP, etc. The existence of this structure allows one to make a saving in time (or channel capacity) by properly encoding the message sequences into signal sequences. This is already done to a limited extent in telegraphy by using the shortest channel symbol, a dot, for the most common English letter E; while the infrequent letters, Q, X, Z are represented by longer sequences of dots and dashes. This idea is carried still further in certain commercial codes where common words and phrases are represented by four- or five-letter code groups with a considerable saving in average time. The standardized greeting and anniversary telegrams now in use extend this to the point of encoding a sentence or two into a relatively short sequence of numbers.