William Spaniel - Game Theory 101: The Basics

Game Theory 101: The Basics

By William Spaniel

Copyright William Spaniel, 2011.

All rights reserved.

Acknowledgements

I thank Varsha Nair for her revisions as I compiled this book. I am also indebted to Kenny Oyama and Matt Whitten for their further suggestions.

Please report possible errors to . Since this is an electronic book, I will issue corrections whenever appropriate.

Table of Contents

Lesson 1.1: The Prisoners Dilemma and Strict Dominance

Lesson 1.2: Iterated Elimination of Strictly Dominated Strategies

Lesson 1.3: The Stag Hunt, Pure Strategy Nash Equilibria, and Best Responses

Lesson 1.4: Dominance and Nash Equilibrium

Lesson 1.5: Matching Pennies and Mixed Strategy Nash Equilibrium

Lesson 1.6: Calculating Payoffs

Lesson 1.7: Strictly Dominant Mixed Strategies

Lesson 1.8: The Odd Rule and Infinitely Many Equilibria

Final Thought

About the Author

Lesson 1.1: The Prisoners Dilemma and Strict Dominance

The prisoners dilemma is the oldest and most studied game in game theory, and its solution concept is also the simplest. As such, we will start with it.

Two thieves plan to rob an electronics store. As they approach the backdoor, the police arrest them for trespassing. The cops suspect that the pair had planned to break in but lack the evidence to support such an accusation. They therefore require a confession to charge the suspects with the greater crime.

Having studied game theory in college, the interrogator throws them into the prisoners dilemma. He privately sequesters both robbers and tells them the following:

We are currently charging you with trespassing, which calls for a one month jail sentence. I know you were planning on robbing the store, but right now I cannot prove itI need your testimony. In exchange for your cooperation, I will dismiss your trespassing charge, and your partner will be charged to the fullest extent of the lawa twelve month jail sentence.

I am offering your partner the same deal. If both of you confess, your individual testimony is no longer as valuable, and your jail sentence will be eight months each.

If both criminals are self-interested and only care about minimizing their jail time, should they take the interrogators deal?

Solving the Game

The story contains a lot of information. Luckily, we can condense everything we need to know into a simple matrix:

We will use this type of game matrix regularly, so it is important to understand what it means. There are two players in this game. The first players moves (keep quiet and confess) are in the rows, and the second players moves are in the columns; the first players payoffs are listed first for each outcome, and the second players are listed second. For example, if the first player keeps quiet and the second player confesses, then the game ends in the top right set of payoffs, with the first player receiving twelve months of jail time and the second player receiving zero. Finally, as a matter of convention, we refer to the first player as a man and the second player as a woman; this will allow us to utilize pronouns like he and she instead of repeating player 1 and player 2 ad nauseam .

So what is each players optimal strategy? To see the answer, it is best to look at each move in isolation. Look at this from the perspective of player 1. Suppose he knew player 2 would keep quiet. What should he do? Lets check the important information in that context and replace everything that does not matter with a question mark:

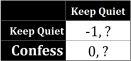
From this, it is clear that player 1 should confess. If he keeps quiet, he will spend one month in jail. But if he confesses, he walks away. Since he prefers less jail time to more jail time, he should confess in this situation. Note that player 2s payoffs are completely irrelevant to player 1s decision in this contextif he knows that she will keep quiet, then he only needs to look at his own payoffs to decide which strategy to pick. Thus, the question marks could be any number at all, and player 1s decision will remain the same.

Now suppose player 1 knew that player 2 would confess. What should he do? Again, the answer is easier to see if we look at the only information that matters here:

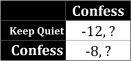
Confession wins a second time: confessing leads to eight months of jail time, whereas silence buys twelve. So player 1 would want to confess if player 2 confesses.

Putting these two pieces of information together, we reach an important conclusionplayer 1 is better off confessing regardless of what player 2 does! Thus, player 1 can effectively ignore whatever he thinks player 2 will do, since confessing gives him less jail time in either scenario.

Now lets take player 2s perspective. Suppose she knew that player 1 will keep quiet, even though we realize he should not. Here is her situation:

As before, player 2 should confess, as he will shave a month off her jail sentence for doing so.

Finally, suppose she knew player 1 will confess. How should she respond?

Unsurprisingly, she should confess and spend four fewer months in jail.

Once more, player 2 is better off confessing regardless of what player 1 does. Thus, we have reached a solution: both players confess, and both players spend eight months in jail. The justice system has triumphed, thanks to the interrogators savviness!

This outcome perplexes a lot of people new to the field of game theory. Looking at the game matrix, they see that the outcome leaves both players better off than the outcome and wonder why the players cannot coordinate on the more efficient outcome. But as we just saw, any promise to keep quiet is unbelievable. Player 1 wants player 2 to keep quiet so when he confesses he walks away freely. The same goes for player 2. As a result, the outcome is inherently unstable, which is why the players ultimately end up in the inferior (but sustainable) outcome.

Meaning of the Numbers

Although there is a large branch of game theory devoted to the study of expected utility, we generally consider each players payoffs as a ranking of his most preferred outcome to his least preferred outcome. In the prisoners dilemma, we assumed that players only wanted to minimize their jail time. Game theory does not force players to believe that is the case, as critics frequently claim. Instead, game theory analyzes what should happen given what players desire. So if players only want to minimize jail time, we could use the negative number of years spent in jail as their payoffs. This preserves their individual orderings over outcomes, as the most preferred outcome is worth 0, the least preferred outcome is -10, and everything else logically follows in between.

Interestingly, the cardinal values of the numbers are irrelevant to the outcome of the game. For example, suppose we changed the matrix to this:

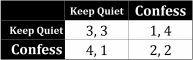
Here, we have replaced the months of jail time with an ordering of most to least preferred outcomes, with 4 representing a players most preferred outcome and 1 representing a players least preferred outcome. In other words, player 1 would most like to reach the outcome, then the outcome, then the outcome, then the outcome.