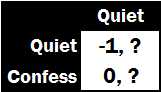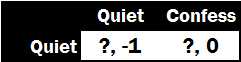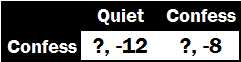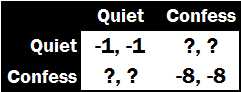William Spaniel - Game Theory 101: The Complete Textbook

The story contains a lot of information. Luckily, we can condense everything we need to know into a simple matrix:

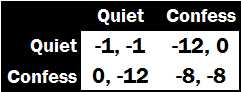
We will use this type of game matrix regularly, so it is important to understand how to interpret it. There are two players in this game. The first players strategies (keep quiet and confess) are in the rows, and the second players strategies are in the columns. The first players payoffs are listed first for each outcome, and the second players are listed second. For example, if the first player keeps quiet and the second player confesses, then the game ends in the top right set of payoffs; the first player receives twelve months of jail time and the second player receives zero. Finally, as a matter of convention, we refer to the first player as a man and the second player as a woman; this will allow us to utilize pronouns like he and she instead of endlessly repeating player 1 and player 2.

Which strategy should each player choose ? To see the answer, we must look at each move in isolation. Consider the game from player 1s perspective. Suppose he knew player 2 will keep quiet. How should he respond?

L ets focus on the important information in that context. Since player 1 only cares about his time in jail, we can block out player 2s payoffs with question marks:

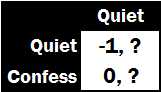
P layer 1 should confess. If he keeps quiet, he will spend one month in jail. But if he confesses, he walks away. Since he prefers less jail time to more jail time, confession produces his best outcome.

Note that player 2s payoffs are completely irrelevant to player 1s decision in this contextif he knows that she will keep quiet, then he only needs to look at his own payoffs to decide which strategy to pick. Thus, the question marks could be any number at all, and player 1s optimal decision given player 2s move will remain the same.

On the other hand, suppose player 1 knew that player 2 will confess. What should he do? Again, the answer is easier to see if we only look at the relevant information:

C onfession wins a second time: confessing leads to eight months of jail time, whereas silence buys twelve. So player 1 would want to confess if player 2 confesses.

Putting these two pieces of information together, we reach an important conclusionplayer 1 is better off confes sing regardless of player 2s strategy! Thus, player 1 can effectively ignore whatever he thinks player 2 will do, since confessing gives him less jail time in either scenario.

L ets switch over to player 2s perspective. Suppose she knew that player 1 will keep quiet, even though we realize he should not. Here is her situation:

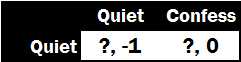
As before, player 2 should confess , as she will shave a month off her jail sentence if she does so.

Finally, suppose she knew player 1 will confess. How should she respond?

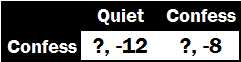
Unsurprisingly, she should confess and spend four fewer months in jail.

Once more, player 2 prefers confessing regardless of what player 1 does. Thus, we have reached a solution: both players confess, and both players spend eight months in jail. The justice system has triumphed, thanks to the interrogators savviness.

This outcome perplexes a lot of people new to the field of game theory. Compare the outcome to the outcome:

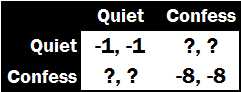
Looking at the game matrix, people see that the outcome leaves both players better off than the outcome. They then wonder why the players cannot coordinate on keeping quiet. But as we just saw, promises to remain silent are unsustainable. Player 1 wants player 2 to keep quiet so when he confesses he walks away free. The same goes for player 2. As a result, the outcome is inherently unstable. Ultimately, the players finish in the inferior (but sustainable) outcome.