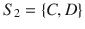Introduction
This chapter first analyzes how to represent games in normal form (using matrices) and in extensive form (using game trees). We afterwards describe how to systematically detect strictly dominated strategies , i.e., strategies that a player would not use regardless of the action chosen by his opponents.
In particular, we say that player
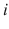
finds strategy
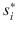
as strictly dominated by another strategy
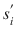
if
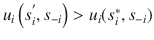
for every strategy profile
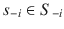
, where
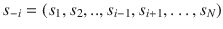
represents the profile of strategies selected by player
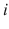
s opponents, i.e., a vector with
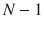
components. In words, strategy
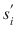
strictly dominates
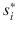
if it yields a strictly higher utility than strategy
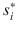
regardless of the strategy profile that player i s rival choose.
Since we can anticipate that strictly dominated strategies will not be selected by rational players, we apply the Iterative Deletion of Strictly Dominated Strategies (IDSDS) to predict players behavior. We elaborate on the application of IDSDS in games with two and more players, and in games where players are allowed to choose between two strategies, between more than two strategies, or a continuum of strategies. In some games, we will show that the application of IDSDS is powerful, as it rules out dominated strategies and leaves us with a relatively precise equilibrium prediction, i.e., only one or two strategy profiles surviving the application of IDSDS. In other games, however, we will see that IDSDS does not have a bite because no strategies are dominated; that is, a strategy does not provide a strictly lower payoff to player
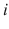
regardless of the strategy profile selected by his opponents (it can provide a higher payoff under some of his opponents strategies). In this case, we wont be able to offer an equilibrium prediction, other than to say that the entire game is our most precise equilibrium prediction! In subsequent chapters, however, we explore other solution concepts that provide more precise predictions that IDSDS.
Finally, we study the deletion of weakly dominated strategies does not necessarily lead to the same equilibrium outcomes as IDSDS, and its application is in fact sensible to deletion order. We can apply the above definition of strictly dominated strategies to define weakly dominated strategies. Specifically, we say that strategy
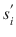
weakly dominates
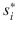
if
Exercise 1From Extensive Form to Normal form Representation-IA
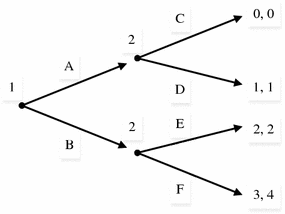
Represent the extensive-form game depicted in Fig. using its normal-form (matrix) representation.
Fig. 1.1
Extensive-form game
Answer
We start identifying the strategy sets of all players in the game. The cardinality of these sets (number of elements in each set) will determine the number of rows and columns in the normal-form representation of the game.
Starting from the initial node (in the root of the game tree located on the left-hand side of the figure), Player 1 must select either strategy A or B , thus implying that the strategy space for player 1,
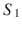
, is:
In the next stage of the game, Player 2 conditions his strategy on player 1s choice, since player 2 observes such a choice before selecting his own. We need to consider that the strategy profile of player 2 ( S 2) must be a complete plan of action (complete contingent plan) . Therefore, his strategy space becomes:
where the first component of every strategy describes how player 2 responds upon observing that player 1 chose A , while the second component represents player 2s response after observing that player 1 selected B . For example, strategy CE describes that player 2 responds with C after player 1 chooses A , but with E after player 1 chooses B .
Using the strategy space of player 1, with only two available strategies S 1 = { A, B }, and that of player 2, with four available strategies S 2 = { CE, CF, DE, DF }, we obtain the
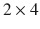
payoff matrix represented in Fig.. For instance, the payoffs associated with the strategy profile where player 1 chooses A and player 2 chooses C if A and E if B , {A, CE}, is (0,0).
Remark : Note that, if player 2 could not observe player 1s action before selecting his own (either C or D ), then player 2s strategy space would be
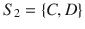












 finds strategy
finds strategy 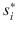 as strictly dominated by another strategy
as strictly dominated by another strategy 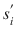 if
if 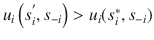 for every strategy profile
for every strategy profile 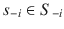 , where
, where 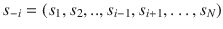 represents the profile of strategies selected by player
represents the profile of strategies selected by player 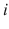 s opponents, i.e., a vector with
s opponents, i.e., a vector with 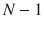 components. In words, strategy
components. In words, strategy 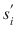 strictly dominates
strictly dominates 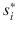 if it yields a strictly higher utility than strategy
if it yields a strictly higher utility than strategy 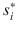 regardless of the strategy profile that player i s rival choose.
regardless of the strategy profile that player i s rival choose.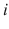 regardless of the strategy profile selected by his opponents (it can provide a higher payoff under some of his opponents strategies). In this case, we wont be able to offer an equilibrium prediction, other than to say that the entire game is our most precise equilibrium prediction! In subsequent chapters, however, we explore other solution concepts that provide more precise predictions that IDSDS.
regardless of the strategy profile selected by his opponents (it can provide a higher payoff under some of his opponents strategies). In this case, we wont be able to offer an equilibrium prediction, other than to say that the entire game is our most precise equilibrium prediction! In subsequent chapters, however, we explore other solution concepts that provide more precise predictions that IDSDS.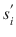 weakly dominates
weakly dominates 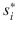 if
if 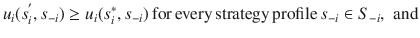

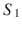 , is:
, is: 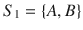
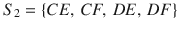
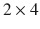 payoff matrix represented in Fig.. For instance, the payoffs associated with the strategy profile where player 1 chooses A and player 2 chooses C if A and E if B , {A, CE}, is (0,0).
payoff matrix represented in Fig.. For instance, the payoffs associated with the strategy profile where player 1 chooses A and player 2 chooses C if A and E if B , {A, CE}, is (0,0).