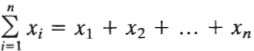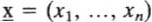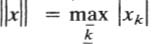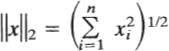GAMES, THEORY
AND APPLICATIONS
GAMES, THEORY
AND APPLICATIONS
L. C. Thomas
School of Management
University of Southampton
DOVER PUBLICATIONS, INC.
Mineola, New York
Copyright
Copyright 1984, 1986 by L. C. Thomas.
All rights reserved.
Bibliographical Note
This Dover edition, first published in 2003, is a slightly corrected, unabridged republication of the 1986 paperback edition of the work originally published by Ellis Horwood/John Wiley, Chichester, London, in 1984.
Library of Congress Cataloging-in-Publication Data
Thomas, L. C.
Games, theory and applications / L.C. Thomas.
p. cm.
... a slightly corrected, unabridged republication of the 1986 paperback edition of the work originally published by Ellis Horwood/John Wiley, Chichester, London, in 1984T.p. verso.
Includes bibliographical references and index.
eISBN 13: 978-0-486-14373-6
1. Game theory. I. Title.
QA269.T58 2003
519.3dc22
2003055658
Manufactured in the United States by Courier Corporation
43237802
www.doverpublications.com
To Carey, Iris, Fred and Glenys,
and in memory of Eunice
Authors Preface
The preface of a book is positioned first, written last, and read little. It should also be the authors guide to and raison dtre for the following manuscript. So here goes.
The theory of games, as a way of modelling problems with two or more decision-makers involved, originated at the end of the Second World War, though the playing of games themselves has been one of the enduring strands in the history of mankind. At the same time as game theory was being developed, new mathematical techniques were being invented in other types of decision-making. This whole area of applicable mathematics has continued to be one of the most active branches of research and development up to the present day. Game theory, despite an uneven reputation during this period, has continued to develop, in depth of understanding and breadth of applications.
Its fascination, for me, is that it is the one area where quite difficult logical ideas can be expressed rigorously, with the minimum of mathematical sophistication. These ideas can be quickly comprehended because there are manifestations of them in real life, with which people are familiar. Thus, of itself, game theory has much to recommend it, apart from its applications. However, it is the applications which are of paramount importance. Games can be used as models of situations as diverse as international conflict, advertising budgets, pricing policy, airport loading fees, and the evolution of animal behaviour. In some cases, the analysis of the game will lead to a specific strategy for each participant being considered as his best way of playing the game: in other games and types of analysis, all that can be done is an exploration of what were the players understanding of each other in order for a certain outcome to occur. So there is something for everyone.
The book evolved from a lecture course I have given for several years to undergraduates at Manchester. The students came from many different departmentsmathematics, science, economics, accountancy, liberal studies, and psychology. Thus, the book assumes a modest mathematical backgroundan ability to differentiate and integrate simple functions, the idea of maxima and minima of functions, familiarity with matrix notation (though not the properties of matrices) and summation signs, and a basic knowledge of probability. Although my upbringing means I like to use theorems and lemmas to structure and point out the important results, proofs are only given where they can be understood with this background, and employ ideas and techniques which are used again in the text.
The books aim is to give an introduction to game theory to as wide a numerate audience as possible. Thus, I do not concentrate on linear programming solution techniques, which would weight it more towards the mathematician; and I treat the economic applications of game theory, which several authors have concentrated on, as only one of several such applications.
give the theory of two-person and n-person games. The remaining chapters are independent of one another, but do use the theory developed in the first few chapters. However, I do point out connections between work in different chapters when they arise. All chapters end with a section of further reading which indicates where one can pursue the ideas of that chapter further, and some problems. I have included solutions to the problems to encourage the reader to attempt them. Doing the problems is the way of proving you understand the ideas in the text.
I am grateful to my colleagues Doug White, Roger Hartley, and Chris Birchenall for many useful conversations. I am especially grateful to Simon French, who taught a course from the draft of this book for a year, and whose comments and corrections of my errors proved very valuable. All remaining errors are deliberate mistakes by me! My thanks are also due to Kate Baker and Bob Lande, who typed the manuscripts with great care, on both sides of the Atlantic in between babies and racquetball championships, respectivelyanything to get away from my handwriting! Finally, my thanks go to my family who taught me the best cooperative game of all while I was writing this book.
L. C. Thomas
Glossary of Symbols
xX | means x is a member of the set X |
xX | means x is not a member of the set X |
{x|....} | is the set of x with the property ... |
ST = | {x|xS or xT} |
ST = | {x|xS and xT} |
ST = | set S is included in set T |
ST = | {x|xS and xT} |
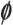
| is the empty set |
#S | the number of elements in the set S |
|x| = | max {x, x} |
x > y | x greater than y |
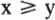
| x greater than or equal to y |
x y y | x not greater than y |
n ! | 1. 2. 3. 4..... (n 1). n |
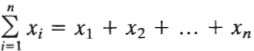
If 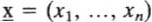
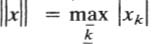
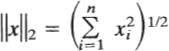
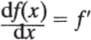
Next page












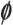
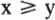
 y
y