Except for the first section, the appendix consists of a diverse selection of further examples of differential games. The solutions are sketched with hints for aid when unusual features or formal difficulties occur.
A1. A HIT PROBABILITY PAYOFF
In certain military games, such as those in Sections A2 and A5, one player, say E , continuously fires a weapon at his opponent. The payoff is to be the total probability of a hit.
The hit probability density p is supposed given: p is a function of the state variables (and conceivably of the control variables also). Thus in a definite partie, p becomes a function p ( t ) of the time, and the probability of a hit in the interim ( t , t + h ) is hp ( t ) + O( h 2).
LEMMA A1. In the above circumstances the game has an integral payoff, and we may take
Proof. Let Q ( t ) be the probability that the target is missed by all fire during (0 , t ).
The probability that the target is missed during (0, t + h ) is the product of the probabilities that it was missed during (0, t ) and ( t , t + h ). Thus if h is small,
Q ( t + h ) = Q ( t )(1 hp ( t ))
or
which in the limit is
Q = pQ .
As Q (0) = 1, we have
Thus the probability of a hit during (0, t ) is 1 Q ( t ) and so is an increasing function of the integral. Then if a strategy renders the integral, say, maximal, it likewise so renders the hit probability.
Note that the formal Value V ( x ) yielded by the solution is not the hit probability, the actual Value. The latter is 1 exp ( V ( x )).
Let us think of the continuous fire as (it actually is) a succession of small shots. It is not hard to show that in two-dimensional space, the hit probability of a single shot varies inversely with the range, the distance from weapon to target, for reasonably large r . Thus p may be taken as a / r for some constant a . In three-dimensional space, correspondingly, p = a / r 2. (The former is used in the two succeeding problems only because it facilitates the formal mathematics.)
A2. THE FIXED BATTERY PURSUIT GAME
Both players have simple motion in a plane. The pursuer P is faster and could capture E readily were he not deterred by a barrage of gunfire assisting E . The firing is continuous and emanates from a battery located at a point O . The instantaneous hit probability is inversely proportional to the distance OP , and its time integral, as in Section A1, is to be the payoff.
Thus P seeks to capture with a minimum chance of being hit; he must choose a course which compromises between a direct chase of E and a wariness of being too close to the battery for too long. Similarly, E must inculcate into his flight from P maneuvering which lures P into lethal proximity to O .
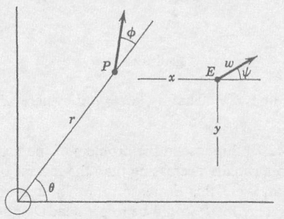
We shall use the polar coordinates r , for P and the rectangular coordinates x , y for E , both systems having the same origin O with the lines = 0 and y = 0 coinciding. The speeds of P and E shall be 1 and w with w < 1, so that w is really the speed ratio of E to P . The control variables and 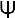 are as in . The KE are thus
are as in . The KE are thus
The payoff is integral with
a being a fixed positive constant. The terminal surface is the set where | PE | = l , a given positive number, and 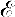 , the set with | PE | /.
, the set with | PE | /.
The solution is obtained almost entirely by pure integration, this example being very exceptional in its freedom from singular phenomena. One singular surface there certainly is: when P , O , E lie on a straight line in this order, the two symmetrical ways that P may skirt O clearly imply a dispersal surface, with an instantaneous mixed strategy.
Our standard method then presents no difficulties (except possibly the common one of deciding the sign of the V i of the initial conditions). From the RPE, it will follow at once that E always travels a straight path. Any route of P , however, lies on a curve:
where c 1,... , c 4, K are constants; K may be of either sign, meaning that for some paths sin, cos, replace sinh, cosh.
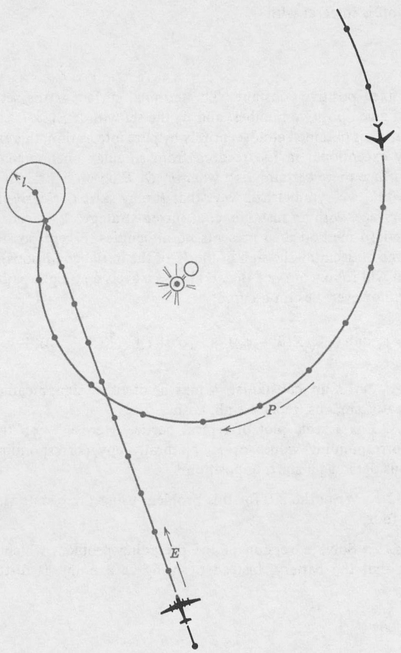
is a scale plot of typical partie. Here w  the dots indicate corresponding values of . Naturally any corresponding pair may be considered as a starting position.
the dots indicate corresponding values of . Naturally any corresponding pair may be considered as a starting position.
Exercise A2.1 . Write the KE for this problem using three state variables instead of four.
Exercise A2.2 . Solve a version of the preceding problem which differs from it in that the battery, instead of being at a point, is distributed uniformly over a line 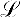 . That is, G = a/d , where d = distance P to
. That is, G = a/d , where d = distance P to 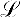 .
.
Research Problem A2.1 . Suppose in the problem of the text we had taken for G a function more rapidly decreasing than the inverse of r . Intuitively it might appear that, were this decrease rapid enough and had E time enough, the best strategy for E would be to get near O and to loiter there. Is this ever actually the case? If so, how is such a problem solved?
A3. OPTIMAL TRAJECTORIES OF GUIDED MISSILES
The design of long-range missile trajectories so as to maximize efficiency is a task amenable to the present methods. We are faced with a one-player game, the payoff or quantity to be optimized usually being the fuel consumption.
Let us look at a prototype case. The coordinates of 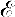 , the state variables, will be such quantities as
, the state variables, will be such quantities as
the positional coordinates of the missile
the velocity components
the yaw angle and other such inclinations
the current weight of the missile (decreasing due to fuel consumption).
The control variables will be, of course, just those quantities regulated by the guidance system.












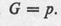
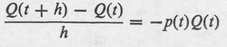
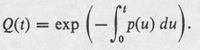
 are as in . The KE are thus
are as in . The KE are thus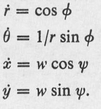
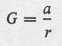
 , the set with | PE | /.
, the set with | PE | /.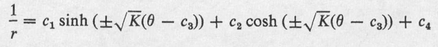
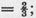 the dots indicate corresponding values of . Naturally any corresponding pair may be considered as a starting position.
the dots indicate corresponding values of . Naturally any corresponding pair may be considered as a starting position. . That is, G = a/d , where d = distance P to
. That is, G = a/d , where d = distance P to