Optimal Control Theory An Introduction Donald E. Kirk Professor Emeritus of Electrical EngineeringSan Jos State UniversitySan Jos, California Dover Publications, Inc.
Mineola, New York Copyright Copyright 1970, 1998 by Donald E. Kirk All rights reserved. Bibliographical Note This Dover edition, first published in 2004, is an unabridged republication of the thirteenth printing of the work originally published by Prentice-Hall, Inc., Englewood Cliffs, New Jersey, in 1970. Solutions Manual Readers who would like to receive Solutions to Selected Exercises for this book may request them from the publisher at the following e-mail address: Library of Congress Cataloging-in-Publication Data Kirk, Donald E., 1937 Optimal control theory : an introduction / Donald E. cm. cm.
Originally published: Englewood Cliffs, N.J. : Prentice-Hall, 1970 (Prentice-Hall networks series) Includes bibliographical references and index. ISBN-13: 978-0-486-43484-1 (pbk.) ISBN-10: 0-486-43484-2 (pbk.) 1. Control theory. 2. I. Title. Title.
QA402.3.K52 2004 003.5dc22 2003070111 Manufactured in the United States by Courier Corporation
43484204
www.doverpublications.com Preface Optimal control theorywhich is playing an increasingly important role in the design of modern systemshas as its objective the maximization of the return from, or the minimization of the cost of, the operation of physical, social, and economic processes. This book introduces three facets of optimal control theorydynamic programming, Pontryagin's minimum principle, and numerical techniques for trajectory optimizationat a level appropriate for a first- or second-year graduate course, an undergraduate honors course, or for directed self-study. A reasonable proficiency in the use of state variable methods is assumed; however, this and other prerequisites are reviewed in . In the interest of flexibility, the book is divided into the following parts: Part I: Describing the System and Evaluating Its Performance
() Part II: Dynamic Programming
() Part III: The Calculus of Variations and Pontryagin's Minimum Principle
() Part IV: Iterative Numerical Techniques for Finding Optimal Controls and Trajectories
() Part V: Conclusion
() Because of the simplicity of the concept, dynamic programming ( are designed to introduce additional topics as well as to illustrate the basic concepts. My experience indicates that it is possible to discuss, at a moderate pace, in a one-quarter, four-credit-hour course. This material provides adequate background for reading the remainder of the book and other literature on optimal control theory.
To study the entire book, a course of one semester's duration is recommended. My thanks go to Professor Robert D. Strum for encouraging me to undertake the writing of this book, and for his helpful comments along the way. I also wish to express my appreciation to Professor John R. Ward for his constructive criticism of the presentation. Professor Charles H.
Rothauge, Chairman of the Electrical Engineering Department at the Naval Postgraduate School, aided my efforts by providing a climate favorable for preparing and testing the manuscript. I thank Professors Jose B. Cruz, Jr., William R. Perkins, and Ronald A. Rohrer for introducing optimal control theory to me at the University of Illinois; undoubtedly their influence is reflected in this book. The valuable comments made by Professors James S.
Demetry, Gene F. Franklin, Robert W. Newcomb, Ronald A. Rohrer, and Michael K. Sain are also gratefully acknowledged. D. T. T.
Cowdrill and Lcdr. R. R. Owens, USN. Perhaps my greatest debt of gratitude is to the students whose comments were invaluable in preparing the final version of the book. DONALD E.
KIRK Carmel, CaliforniaContents PART I: DESCRIBING THE SYSTEM AND EVALUATING
ITS PERFORMANCE IDescribing the System
and
Evaluating Its PerformanceIntroduction Classical control system design is generally a trial-and-error process in which various methods of analysis are used iteratively to determine the design parameters of an acceptable system. Acceptable performance is generally defined in terms of time and frequency domain criteria such as rise time, settling time, peak overshoot, gain and phase margin, and bandwidth. Radically different performance criteria must be satisfied, however, by the complex, multiple-input, multiple-output systems required to meet the demands of modern technology. For example, the design of a spacecraft attitude control system that minimizes fuel expenditure is not amenable to solution by classical methods. A new and direct approach to the synthesis of these complex systems, called optimal control theory, has been made feasible by the development of the digital computer. The objective of optimal control theory is to determine the control signals that will cause a process to satisfy the physical constraints and at the same time minimize (or maximize) some performance criterion.
Later, we shall give a more explicit mathematical statement of the optimal control problem, but first let us consider the matter of problem formulation. 1.1 PROBLEM FORMULATION The axiom A problem well put is a problem half solved may be a slight exaggeration, but its intent is nonetheless appropriate. In this section, we shall review the important aspects of problem formulation, and introduce the notation and nomenclature to be used in the following chapters. The formulation of an optimal control problem requires: 1. A mathematical description (or model) of the process to be controlled. 2.
A statement of the physical constraints. 3. Specification of a performance criterion. The Mathematical Model A nontrivial part of any control problem is modeling the process. The objective is to obtain the simplest mathematical description that adequately predicts the response of the physical system to all anticipated inputs. Our discussion will be restricted to systems described by ordinary differential equations (in state variable form).
Thus, if 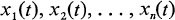 are the state variables (or simply the states) of the process at time t, and
are the state variables (or simply the states) of the process at time t, and 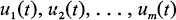 are control inputs to the process at time t, then the system may be described by n first-order differential equations
are control inputs to the process at time t, then the system may be described by n first-order differential equations 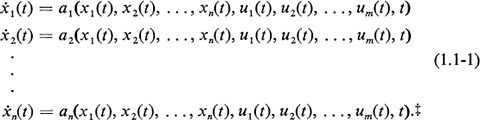 We shall define
We shall define 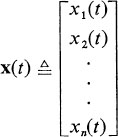 as the state vector of the system, and
as the state vector of the system, and 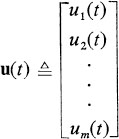 as the control vector. The state equations can then be written
as the control vector. The state equations can then be written  where the definition of a is apparent by comparison with .
where the definition of a is apparent by comparison with .  Figure 1-1 A simplified control problem is to be driven in a straight line away from point O. The distance of the car from O at time t is denoted by d(t). To simplify the model, let us approximate the car by a unit point mass that can be accelerated by using the throttle or decelerated by using the brake. The differential equation is
Figure 1-1 A simplified control problem is to be driven in a straight line away from point O. The distance of the car from O at time t is denoted by d(t). To simplify the model, let us approximate the car by a unit point mass that can be accelerated by using the throttle or decelerated by using the brake. The differential equation is
Next page












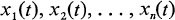 are the state variables (or simply the states) of the process at time t, and
are the state variables (or simply the states) of the process at time t, and 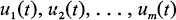 are control inputs to the process at time t, then the system may be described by n first-order differential equations
are control inputs to the process at time t, then the system may be described by n first-order differential equations 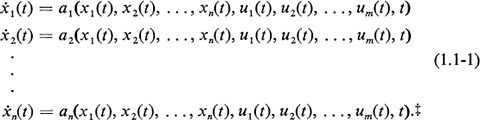 We shall define
We shall define 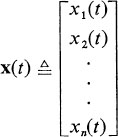 as the state vector of the system, and
as the state vector of the system, and 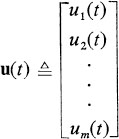 as the control vector. The state equations can then be written
as the control vector. The state equations can then be written  where the definition of a is apparent by comparison with .
where the definition of a is apparent by comparison with .  Figure 1-1 A simplified control problem is to be driven in a straight line away from point O. The distance of the car from O at time t is denoted by d(t). To simplify the model, let us approximate the car by a unit point mass that can be accelerated by using the throttle or decelerated by using the brake. The differential equation is
Figure 1-1 A simplified control problem is to be driven in a straight line away from point O. The distance of the car from O at time t is denoted by d(t). To simplify the model, let us approximate the car by a unit point mass that can be accelerated by using the throttle or decelerated by using the brake. The differential equation is