Denise Gaskins - Addition & Subtraction

Math You Can Play Series

Book Two

Addition & Subtraction

Math Games for Elementary Students

Kindergarten to Fourth Grade

Denise Gaskins

Copyright 2015 Denise Gaskins

Ebook Version 1.61

All rights reserved.

Tabletop Academy Press

tabletopacademy.net

Readers Love Denises Playful Math Books

These games are great for using and practicing maths skills in a context in which there is some real motivation to do so. I love how they provide opportunities to explore a wide variety of approaches, including number bonds and logical thinking.

My children are always pleased, even excited, when I suggest one of these games. Sometimes they even ask to play them unprompted!

Miranda Jubb, online reader review

It revolutionized our homeschool this year.

Caitlin Fitzpatrick Curley, My-Little-Poppies.com

I have played several of these games with my son, and each one was met with delight on his part and the sharing of delightful conversation about numbers and thinking between us.

I love what Gaskins has to say about working with your children as opposed to simply assigning them work to do. This sums up the philosophy that I try to keep forefront in our home.

Highly, highly recommended.

Amy, Hope Is the Word blog

Wonderful games for elementary students. The author includes a link for printable game boards, ensuring that I don't spend more time making games than playing them. Variations for each game = SO many ways to explore numbers. You will love this book.

Marisa, online reader review

Free Playful Math Newsletter

Want to help your kids learn math? Join my free newsletter for monthly (well, most months) activity ideas. And youll be among the first to hear about new books, revisions, and sales or other promotions.

tabletopacademy.net/mathnews

Contents

Preview Game: Tiguous

Math Concepts: addition, subtraction, multistep calculation.

Players: two or more.

Equipment: game board, three six-sided dice, pencil or marker(s), scratch paper for keeping score.

[Picture below] Which square would you mark?

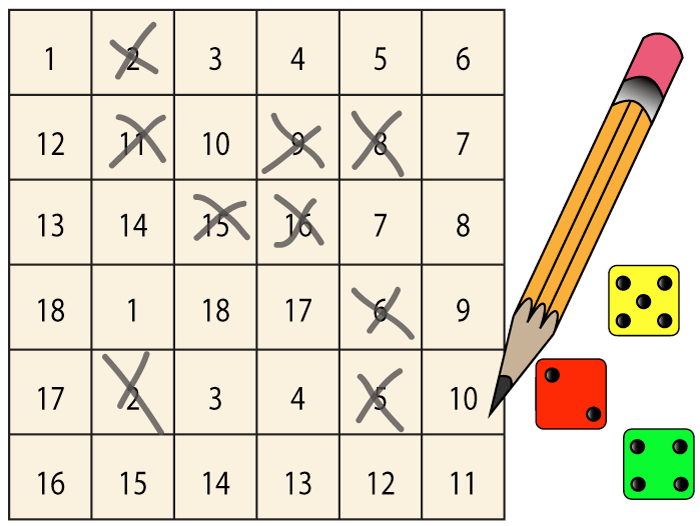
Set-Up

You can print the Tiguous game board from the Number Game Printables Pack, download the Contig, Jr. game from Terry Kawass MathWire website, or have your children make their own game board.

tabletopacademy.net/free-printables

mathwire.com/games/contigjr.pdf

If students make their own board, they can arrange the numbers however they like:

Draw a 6 6 grid of squares, each big enough for a two-digit number.

The first player writes the number one in any square. The next chooses a square for the number two. Players take turns writing the numbers 118 anywhere they wish, one number per square.

After eighteen, the next player goes back to one, and the turns continue until the board is full.

How to Play

On your turn, roll all three dice. If any die falls off the table or lands at a slant, all three dice must be rolled again. Do not touch the dice with your hands after they are rolled, though you may use a pencil or marker to scoot them next to each other.

Add or subtract these three numbers in a two-step equation that equals the number in any unmarked square on the game board. Think of as many possible combinations as you can, in order to choose the highest-scoring square. Mark your answer on the game board with a large X. At the same time, say out loud how you calculated the number.

You score 1 point for the square you marked, plus 1 point for each already-marked square that is touching (contiguous to) any side or corner of your numbers square. The maximum score for any turn is 9 points. If all the numbers you can make have already been marked, you score a zerobut if anyone else can find a valid calculation using your dice, that player may challenge you, mark the square, and steal those points.

If another player thinks you made an arithmetic mistake, that person may challenge your answer before the next player rolls the dice. If your answer was wrong, the challenger takes the points you would have won, and you score zero. If your calculation is correct, you get one bonus point for having withstood the challenge.

Play until each player has had ten turns, or five turns each for three or more players. Whoever has the highest total score wins the game.

Variations

The most common variation I have seen is not to score a point for the marked square. Just score 1 point for each contiguous square that was previously marked, which makes the maximum possible score per turn only 8 points. I strongly prefer the scoring system above, which awards at least 1 point for any valid calculation.

Tiguous-Tac-Toe: Two players mark numbers with X and O, and the first player to get three squares in a row wins. Rows may be vertical, horizontal, or diagonal. For a longer game, try to get four or five in a row.

Multiplayer Extended Game: Keep playing until almost all the numbers are marked. Any player who gets a zero three turns in a row drops out of the game. When the last player gets a third strike, the game is over. There is no bonus for the last player, other than the extra turn(s).

Tournament Rules: Two players per game board. Set a timer, giving each player only thirty seconds for each turn. Think fast! If you do not mark a square within the thirty seconds, your score is zero for that turn. Scores of zero may not be challenged in tournament play, but opponents may challenge arithmetic errors. After each player has ten turns, add up the players scores for that round. Then trade partners, get a new game board, and play another round. After three rounds, award 1st, 2nd, and 3rd place ribbons to the top scorers in each age group/grade level.

History

Tiguous is a simplified version of F. W. Broadbents game Contig, which is played on a larger board and allows the use of multiplication and division. I took the name from an even simpler version by Constance Kamii.

For as long as I can remember, our local homeschool group has held a series of Contig practices every spring. Then we host a school tournament, and the top two players in each grade level proceed to a regional tournament against other public and private school teams.

Math is the beautiful, rich, joyful, playful, surprising, frustrating, humbling, and creative art that speaks to something transcendental.

It is worthy of much exploration and examination because it is intrinsically beautiful, nothing more to say.

Why play the violin? Because it is beautiful!

Why engage in math? Because it, too, is beautiful!

James Tanton

Preface to the Math You Can Play Series

The playful, puzzle-solving side of math has always attracted me. In elementary school, calculations were a tedious chore, but word problems provided the opportunity to try out my deductive powers. High school algebra and geometry were exercises in logical reasoning, and college physics was one story problem after anothergreat fun!

As my children grew, I wanted to share this sort of mathematical play with them, but the mundane busyness of everyday life kept pushing aside my good intentions. Determined to make it happen, I found a way to defeat procrastination: invite friends to bring their kids over for a math playdate. We grappled with problems, solved puzzles, and shared games. Skeptical at first, the kids soon looked forward to math club. When that gang grew up and moved on, their younger siblings came to play, and others after them. Sometimes we met weekly, sometimes monthly or just off and on. At our house, at the library, in the park more than twenty years of playing math with kids.