Footnotes
1 David Sklansky - The Theory of Poker, Chapter 23: The Psychology of Poker discusses multiple level poker thinking.
2 Colin F. Camerer - Behavioral Game Theory, pp.16-20 and pp.209-218.
3 Brit Grosskopf and Rosemarie Nagel - The Two-Person BeautyContest.
http://erl.tamu.edu/bgrosskopf/sdarticle.pdf
4 This is a potential explanation for why so few people pick zero in the n-person game.
5 The term zero-sum means that the payoffs to each player sum to zero, or equivalently, to any constant number. Poker is zero-sum because the winnings of one player must necessarily be the losses of another. The case with more than 2 players (known as n-player game theory) is more complicated. This is because players can improve their payoffs by forming alliances amongst each other. Explicit collusion is of course forbidden in poker. However, two players can form an implicit alliance in limit poker by having one player bet and the second player raise, cutting down the odds received by the other players and forcing them to fold more hands. The trouble with n-player game theory is that there are many such alliances that can be formed and must be considered. For more on this issue, see Bill Chen and Jerrod Ankenman - TheMathematics of Poker, Chapter 29: Threes a Crowd: Multiplayer Games.
6 The theory of two person zero-sum games began with John von Neumann and Oskar Morgenstern - The Theory of Games and EconomicBehavior. They showed how to optimally play such games with their minimax theorem, essentially the final word on how to optimally play a two-person zero-sum game. They were also some of the first people to attempt to apply these ideas to some simple versions of poker.
7 Bill Chen and Jerrod Ankenman christened this concept alpha. See The Mathematics of Poker, p.113. However, the relationship has been known for a long time. See, for example, David Sklansky - The Theoryof Poker, Chapter 19: Game Theory and Bluffing. Also see Appendix B: Game Theory starting on page 383.
8 This is named after John Forbes Nash who showed that there is an optimal way to play any n-person, finite game. In the case of a two person zero-sum game, the Nash equilibrium is equivalent to the minimax theorem.
9 Polaris has been created by the Computer Poker Research Group at the University of Alberta.
http://poker.cs.ualberta.ca/
10 Darse Billings et al. - Approximating Game-Theoretic OptimalStrategies for Full-scale Poker.
http://webdocs.cs.ualberta.ca/~games/poker/publications/IJCAI03.pdf
11 The information in this paragraph is taken from an article by Bryce Paradis on poker robots in the Two Plus Two Online Magazine.
12 This model is known as the U[0,1] model and goes back as far as John von Neumann and Oskar Morgenstern - The Theory of Games andEconomic Behavior.
13 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, Chapter 10: Facing The Nemesis: Game Theory.
14 Sonias homepage is on http://pokerparadime.com/.
15 Approximately 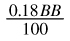 over 730,000 hands. Its actually very impressive that Polaris manages to lose so little against Sonia; most humans lose much more. It shows that any mistakes Polaris is making are worth relatively little in terms of EV for Sonias potential exploitations. This provides strong evidence that Polariss strategy isvery good and worth studying further. http://pokerparadime.com/MessageBoard?messageid=158
over 730,000 hands. Its actually very impressive that Polaris manages to lose so little against Sonia; most humans lose much more. It shows that any mistakes Polaris is making are worth relatively little in terms of EV for Sonias potential exploitations. This provides strong evidence that Polariss strategy isvery good and worth studying further. http://pokerparadime.com/MessageBoard?messageid=158
16 Mike Caro - Caros Book of Poker Tells.
17 Nesmith C. Ankeny - Poker Strategy, p.28, Table 2.3.
18 This is not as true in jacks-or-better to open draw poker played with a joker which would either count as an ace or could be used to complete a straight or a flush. This game was widely played in the cardrooms of California before the legalization of hold em in 1987. See Mason Malmuth - Winning Concepts in Draw and Lowball for more information.
19 David Sklansky - The Theory of Poker, The Cost of Giving Your Hand Away, p.63.
20 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, p.96.
21 Probabilities derived from Nesmith C. Ankeny - Poker Strategy, p.28, Table 2.3.
22 Chris Ferguson - No-Limit Hold Em: How to Bet, printed in Michael Craig (Editor) - The Full Tilt Poker Strategy Guide, p.18.
23 This is known as a belief in the law of small numbers, as humans overestimate the likelihood that even a small sample represents the process that it is drawn from. This is related to the well known gamblers fallacy where roulette players wait for a long string of either red or black before placing a large bet on the other color, erroneously reasoning that the other color is due. Amos Tversky and Daniel Kahneman - Belief in the Law of Small Numbers, printed in Daniel Kahneman, Paul Slovic, and Amos Tversky (Editors) - Judgment UnderUncertainty: Heuristics and Biases, pp.23-31. Tversky and Kahnemans work is based on finding common errors in decision making that violate the norms of statistical and economic theory, some of which will be
discussed in Risk Preferences: From EV to EU and Psychological Biases starting on pages 278 and 299 respectively.
24 The first time I read about this concept was in Bob Ciaffone - ImproveYour Poker, pp.106-107, but the first time it appeared in print was in David Sklansky and Mason Malmuth - Hold em Poker for AdvancedPlayers.
25 Chris Ferguson - No-Limit Hold Em: How to Bet, printed in Michael Craig (Editor) - The Full Tilt Poker Strategy Guide, p.20.
26 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, Chapter 21: A Case Study: Using Game Theory.
27 Nick Christenson and Russell Fox - Winning Strategies for No-LimitHoldem. They devote Part 2 of their book (just under a hundred pages) to bet sizing.
28 Chris Ferguson advocates the same strategy, After the flop, I ignoremy actual holding and decide how much Im going to bet if I bet. Chris Ferguson - No-Limit Hold Em: How to Bet, printed in Michael Craig (Editor) - The Full Tilt Poker Strategy Guide, p.24.
29 Nick Grudzien and Geoff Herzog - Winning In Tough Hold em Games is a good starting point for figuring out individual hand thresholds in preflop limit hold em.
30 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, p.266; Chris Ferguson - No-Limit Hold Em: How to Bet, printed in MichaelCraig (Editor) - The Full Tilt Poker Strategy Guide, p.20. These authors are discussing the game of no-limit hold em. However, the arguments for never limping first-in for limit hold em are even stronger. In general, implied odds are a much greater consideration in no-limit than in limit (assuming large stack sizes) since in limit the size of future bets are restricted by the rules of the game. Therefore, its much more about winning the current pot than maximizing the chances of winning future bets. For this reason, raising first-in is imperative as it gives you a chance of winning the pot outright. The only exception is playing first-in as the small blind versus the big blind where there are some arguments for calling over raising (especially in games where the small blind is two-thirds the size of the big blind). This situation will be discussed later on.
31 There is a possible exception to the above. In games where a bet and four raises is allowed, as opposed to the more common bet and three, it can make sense to fold your weakest raising hands for two more bets after a first-in raise. The reason should be obvious.









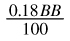 over 730,000 hands. Its actually very impressive that Polaris manages to lose so little against Sonia; most humans lose much more. It shows that any mistakes Polaris is making are worth relatively little in terms of EV for Sonias potential exploitations. This provides strong evidence that Polariss strategy isvery good and worth studying further. http://pokerparadime.com/MessageBoard?messageid=158
over 730,000 hands. Its actually very impressive that Polaris manages to lose so little against Sonia; most humans lose much more. It shows that any mistakes Polaris is making are worth relatively little in terms of EV for Sonias potential exploitations. This provides strong evidence that Polariss strategy isvery good and worth studying further. http://pokerparadime.com/MessageBoard?messageid=158