Published by Icon Books Ltd, Omnibus Business Centre, 39-41 North Road, London N7 9DP
email:
www.introducingbooks.com
ISBN: 978-184831-761-1
Text and illustrations copyright 2013 Icon Books Ltd
The author and artist have asserted their moral rights.
Originating editor: Richard Appignanesi
No part of this book may be reproduced in any form, or by any means, without prior permission in writing from the publisher.
Contents
What is Logic?
Nothing is more natural to conversation than argument. We try to convince the person we are arguing with that we are right, that our conclusion follows from something that they will accept. It would be no good if we could not tell when one thing followed from another. What is often passed off in conversation as an argument does not fit the bill.
ALL PROPERTY IS THEFT.SO ALL THEFT IS PROPERTY.THEREFORE THESE PEARLS ARE MINE.
This is clearly rubbish because there is nothing to link the truth of the conclusion to the truth of the supporting claims. What we need is to ensure that the truth of the supporting claims is preserved by the argument. Logic is quite simply the study of truth-preserving arguments.
Studying Sentences
The Greek philosopher Aristotle (384322 BC) first gave us the idea of a tool (organon) to argue convincingly. This study included grammar, rhetoric and a theory of interpretation, as well as logic. The first thing Aristotle does is discuss sentences.
SENTENCES COME IN THREE TYPESIN EACH OF THESE TYPES WE ARE SAYING THAT SOMETHING OR SOME THINGS ARE OF A CERTAIN KIND.
1. Singular: Socrates is a man.
2. Universal: Every man is mortal.
3. Particular: Some men are mortal.
The objects we talk about (e.g., nouns like Socrates and tables; abstract nouns like walking; and pronouns like someone and everyone) Aristotle calls the subject of the sentence.
What we say about the subject of the sentence (e.g., verbs like is eating and has fallen; adjectives like is difficult; and nouns like man in things like Socrates is a man) Aristotle called the predicate.
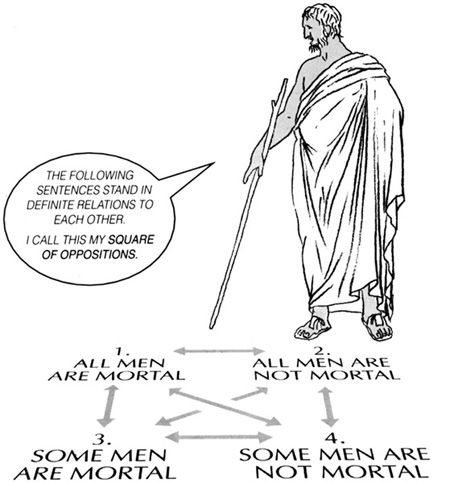
The Square off Oppositions
Aristotle noticed that the truth of some subject-predicate sentences has an effect on the truth of other subject-predicate sentences.
THE FOLLOWING SENTENCES STAND IN DEFINITE RELATIONS TO EACH OTHER. I CALL THIS MY SQUARE OF OPPOSITIONS.
Sentences and cannot both be true.
The diagonal statements and are known contradictories. As long as there are men, one of them has to be true but never both the truth of one guarantees that the other is false.
The same is true for the diagonal statements and
Sentences and can both be true. If is true then must be true, but being true does not mean that must be true.
Similarly with 2 and 4. The same relation holds between All men are mortal and Socrates is mortal.
The Syllogism
Using the square of oppositions, Aristotle noticed a mysterious fact. Take a sentence like Socrates is a man. If an argument of three statements is built where the subject of the first statement is the predicate of the second (call these the premises) and the third statement is composed of the remaining terms (call this the conclusion), then the truth of the conclusion is guaranteed by the truth of the premises.
THIS SCHEMA I CALL A SYLLOGISM. WE CAN USE IT TO SEE WHY ONE ARGUMENT IS TRUE AND ANOTHER FALSE.
Aristotle forgot conditional statements that have more than one predicate, e.g.,
If Socrates is a man, then Socrates is mortal.
We now have two reasons why the argument Arsenal are in London, therefore Arsenal will win the cup is false. The first comes from what is actually said. There is no way that the facts that I support Arsenal and that Arsenal are in London are enough to guarantee that Arsenal will win the cup. But there is also the formal reason that the predicate of the first premise is not the subject of the second.
YES, BUT THIS IS VALID 1. If I support Arsenal, then they will win the cup. 2. I do support Arsenal, so ... 3. Arsenal will win the cup. IT IS STILL FALSE BECAUSE VALIDITY ONLY GRARANTEES THE TRUTH OF THE CONCLUSION IF THE PREMISES ARE TRUE. IN YOUR EXAMPLE THE PREMISES ARE FALSE SO THE CONCLUSION REMAINS FALSE.SO WHAT GOOD DOES THIS FORMALIZATION DO US?YOULL SEE.
Connective Logic
About a hundred years later, Chrysippus of Soli (c.280c.206 BC) changed the focus of logic from single subject-predicate statements to complex statements such as: Socrates is a man and Zeno is a man. This was a major achievement. It was said, If the gods used logic, it would be the logic of Chrysippus. As we shall see, the same is true of us humans, but it took us a couple of millennia to catch on.
WITH WORDS LIKE AND, OR AND IFTHEN, DIFFERENT STATEMENTS CAN BE JOINED TOGETHER AND THE TRUTH OF THE WHOLE WILL DEPEND EXCLUSIVELY ON THE TRUTH OF THE PARTS.
Each of these connectives has a unique way of combining the truth of the parts into the truth of the whole.
For example the or connective and only the or connective can be used in the following way.
Either Muhammad will go to the mountain or the mountain will go to Muhammad. Muhammad did not go to the mountain, therefore the mountain went to Muhammad.
USING MY DEFINITIONS FOR CONNECTIVES, I CAN SHOW HOW TO DERIVE VARIOUS STATEMENTS WHOSE TRUTH IS ALWAYS GUARANTEED BY THE TRUTH OF THE INITIAL STATEMENT.
Chrysippus had no real impact on the history of logic for at least the next 1,500 years, not least because his writings were lost and his ideas known only by second-hand reports, but also because Aristotle became the darling of the Catholic Church.
Leibnizs Law
For the next 2,000 years, logicians came up with an ever increasing number of syllogisms, some including more than two premises. The logician was a kind of alchemist playing around with concepts to get valid arguments. Eventually, a method in this madness was provided by Gottfried Leibniz (16461716).
Leibniz came up with the idea of treating statements like equations in algebra. Equations use the equality sign = to say that two sides must have the same numerical value,