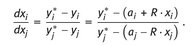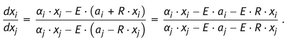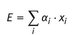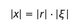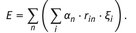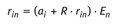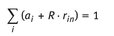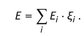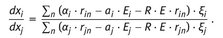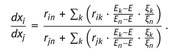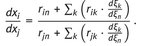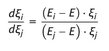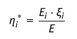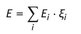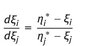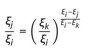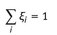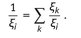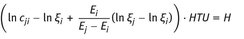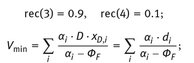Alfons Vogelpohl - Distillation
Here you can read online Alfons Vogelpohl - Distillation full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2017, publisher: De Gruyter, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Distillation
- Author:
- Publisher:De Gruyter
- Genre:
- Year:2017
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Distillation: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Distillation" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Alfons Vogelpohl: author's other books
Who wrote Distillation? Find out the surname, the name of the author of the book and a list of all author's works by series.
Distillation — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Distillation" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
The basic differential equation for the concentration profiles in distillation arrives from and division follows
(A.1)
Insertion of the equilibrium yields
The denominator in
transforms on the basis of the matrix
to
(A.3)
Replacing (see )
(A.4)
and taking into account
(A.5)
yields
Replacing the | x | on the right side of gives
With follows
Differentiation of the yields
(A.9)
A comparison of and (A.8) finally results in
(A.10)
or by defining an equilibrium equation in analogy to
(A.11)
with
(A.12)
results in
(A.13)
with the solution in analogy to
with the constant j determined by the initial conditions of the transformed concentrations ||.
For a polynary mixture of n components there are ( n 1) independent equations of the form (A.14). The concentrations || again (see ) are calculated using the mass balance equation
(A.15)
in the form
(A.16)
The concentration profiles i = f ( H ) follow from
(A.17)
in analogy to .
Application of the matrix finally yields the concentrations | x |.
In the same way as discussed in may be visualized as distillation lines within the distillation space in form of a polyhedron formed by the nodes and the separation lines or separation planes for a ternary or a polynary mixture, respectively.
(A.18)
Recovery of the key components: rec i = x D,i / x F ,i D / F = d i / f i ;
The unknown variables d 1 , d 2 , d 5 and V min are determined by solving the four as a function of the Number of Transfer Units.
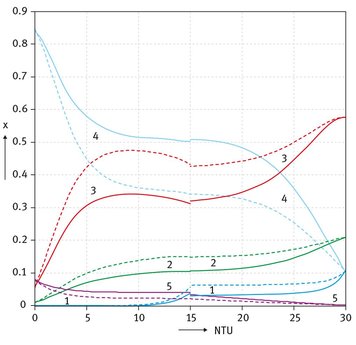
The key components 3 and 4 intersect at the 15th NTU in good agreement with the feed conditions and the feed should be introduced at this position, therefore. Since the method of Shiras indicated that the lowest and the highest boiling component are not distributing, the calculation is extremely sensitive to the chosen concentration of the lowest boiling component in the bottom product and the highest boiling component in the distillate, respectively. The product concentrations applied in are:
. Concentration profiles of the liquid () and the vapour (- -) at limiting flow conditions vs. the number of transfer units ( R = R min = 0.5842)
The dimensions of the column follow from a cost optimisation based on a calculation of the Number of Transfer Un its vs. the reflux ratio. Since the investment costs decrease with an increasing reflux ratio and the energy costs increase with a decreasing reflux ratio, the total costs must show a minimum vs. the reflux ratio [57].
Assuming an average height of a transfer unit ( HTU ) = 0.4 m results in a height of the column H = NTU HTU = 12.00 m with the feed introduced at a height of 6 m.
The diameter of the column follows from fluid dynamic and economic considerations based e.g. on the
- physical and chemical properties of the mixture,
- kind of internals like stages or packings,
- maximum permissible vapour and liquid load of the column,
- ease of operation in case of flow fluctuations,
- economic optimisation.
The final design of the column should be based on specific information given by the supplier of the internals.
Author
Professor
Dr.-Ing. Alfons Vogelpohl
Clausthal University of Technology
Institute for Separation and Process Technology
Leibnizstr. 15
38678 Clausthal-Zellerfeld
Germany
Forbes, R. J.: Of the Art of Distillation from the Beginnings up to the Death of Cellier Blumenthal , Copyright 1948 by E. J. Brill, Leiden, Holland
Underwood, A. J. V.: Distillation Art and Science, Chemistry and Industry , June 23 (1963)
Hausbrand, E.: Die Wirkungsweise der Rectificir- und Destillirapparate , Berlin (1893) cited in [1]
Sorel, E.: La rectification de Ialcool , Paris (1894) cited in [1]
Lewis, W. K., Trans. Am. Inst. Chem. Engrs. , 44 (1922) 329
Lord Rayleigh, Philos. Magazine , 4 (1902) 521
Font size:
Interval:
Bookmark:
Similar books «Distillation»
Look at similar books to Distillation. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Distillation and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.