Beautiful, Simple, Exact, Crazy
Beautiful, Simple, Exact, Crazy: Mathematics in the Real World
Apoorva Khare and Anna Lachowska
Copyright 2015 by Yale University.
All rights reserved.
This book may not be reproduced, in whole or in part, including illustrations, in any form (beyond that copyright permitted by Sections 107 and 108 of the U.S. Copyright Law and except by reviewers for the public press), without written permission from the publishers.
Yale University Press books may be purchased in quantity for educational, business, or promotional use. For information, please e-mail (U.K. office).
Printed in the United States of America.
Library of Congress Control Number: 2015935012
ISBN 978-0-300-19089-2 (pbk. : alk. paper)
A catalogue record for this book is available from the British Library.
This paper meets the requirements of ANSI/NISO Z39.48-1992 (Permanence of Paper).
10 9 8 7 6 5 4 3 2 1
Contents
Preface
The idea for this book arose out of an introductory mathematics course, Mathematics in the Real World, that the authors co-designed and have taught at Yale and Stanford. The purpose of the course is to familiarize students whose primary interests lie outside of the sciences with the power and beauty of mathematics. In particular, we hope to show how simple mathematical ideas can be applied to answer real-world questions.
Thus we see this as a college-level course book that can be used to teach basic mathematics to students with varying skill levels. We discuss specific and relevant real-life examples: population growth models, logarithmic scales, personal finance, motion with constant speed or constant acceleration, computer security, elements of probability, and statistics. Our goal is to combine the right level of difficulty, pace of exposition, and scope of applications for a curious liberal arts college student to study and enjoy.
Additionally, the book could find use by high school students and by anyone wishing to study independently. The prerequisite is only a high school course in algebra. We hope our book can help readers without extensive mathematical training to analyze datasets and real-world phenomena, and to distinguish statements that are mathematically reasonable from those only pretending to be.
Philosophy and goals
Imagine the following dialog in a high school algebra class.
Teacher: Find the sum of the geometric series 1 + 5 + 52 + + 520.
Student (looking out the window and thinking that life is so much bigger than math, and wondering why the class has to suffer through this tedious, long, and pointless computation): Cant we just type it into a calculator?
) to the way we see the world, which might be a source of inspiration for a person of any occupation.
The student we just encountered likely will come to college to major in the humanities or social sciences, and is part of the target audience for this book. Thus, our main goal is to convince our reader that mathematics can be easy, its applications are real and widespread, and it can be amusing and inspiring.
To illustrate, let us return to our geometric series example. Mathematics is known to have formulas for everything, so it is not surprising that it has a formula for the sum 1 + 5 + 52 + + 5n for any natural n. What might be more surprising is that this formula requires no derivatives, integrals, or trigonometric identities and the computation (given in ) takes only one line.
Practical applications of this simple mathematical concept are everywhere: for instance, it governs the payment of mortgages and car loans for millions of people. There is more! Everyone knows that 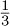 = 0.333333, but the fact that any repeating decimal, say, 0.765765765, can be easily written as a fraction of two integers follows from the formula for the geometric series. The same formula lies in the foundation of Zenos paradox of Achilles and a tortoise, covered in under a parabolic arc. Why should we care? If understanding history is a good enough reason, we can recall that by some accounts, Archimedes also took part in the defense of his town of Syracuse during the siege by the Romans (214-212 BC), and might have used his computation to design a parabolic mirror to set the enemys fleet on fire. Now, fast-forward to the twentieth century. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension was the title of the article, published in Science in 1967 by the French-American mathematician Benoit Mandelbrot, that opened a new area of study fractal geometry. The answer to the question in the title depends on how closely we look, and the closer we look, the greater the coasts length becomes. The same is true for many fractal curves that are easy to describe in words but impossible to draw precisely. One of the central tools used to understand these objects is the geometric series.
= 0.333333, but the fact that any repeating decimal, say, 0.765765765, can be easily written as a fraction of two integers follows from the formula for the geometric series. The same formula lies in the foundation of Zenos paradox of Achilles and a tortoise, covered in under a parabolic arc. Why should we care? If understanding history is a good enough reason, we can recall that by some accounts, Archimedes also took part in the defense of his town of Syracuse during the siege by the Romans (214-212 BC), and might have used his computation to design a parabolic mirror to set the enemys fleet on fire. Now, fast-forward to the twentieth century. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension was the title of the article, published in Science in 1967 by the French-American mathematician Benoit Mandelbrot, that opened a new area of study fractal geometry. The answer to the question in the title depends on how closely we look, and the closer we look, the greater the coasts length becomes. The same is true for many fractal curves that are easy to describe in words but impossible to draw precisely. One of the central tools used to understand these objects is the geometric series.
This is just a glimpse of the scope of applications of one simple mathematical idea from personal finance, to philosophical puzzles, to fractals, objects of such breathtaking beauty that they make the boundary between art and science disappear.
This example encapsulates our philosophy for the book: we would like to show that there is a lot of simple mathematics relevant to peoples everyday lives and their creative aspirations.
There is a way to teach a future artist, and there is a way to teach a layperson to appreciate art. In the latter case, the student is not required to be able to draw and paint like a master, but only to see the beauty in the works of others. Our intention for this book is more ambitious: we hope that it can serve as a guide to the world of mathematics, and also as an inspiration for readers to try their hand at developing and solving mathematical models for their own needs. From there it is only one more step to seeing the world from a mathematical point of view.
The book includes many examples and practice problems designed to gradually build students proficiency and encourage their involvement with the material. The ultimate goal is to make even the students who are numerically shy at the start of a course comfortable applying their mathematical skills in a wide range of situations, from solving puzzles to analyzing statistical data.
We also hope that they become math-friendly, admitting that mathematics can be interesting and cool. We feel that such comfort levels are indeed achieved when we teach this course at Yale and Stanford based on our discussions with students, their exams and homework, and their feedback from the course.
Contents and structure
Here are the most important features that distinguish our approach.
First, we neither discuss nor assume any knowledge of calculus or trigonometry. There are quite a few simple concepts in mathematics that do not depend on this particular knowledge but have enormous importance in the real world, as a vast number of pertinent applications show.
Second, our preference is for a self-contained linear exposition, devoid of digressions and asides. We also refrain from presenting an overload of pictures, data analysis, or complicated examples. This book should be viewed as supporting material for a first course in college-level mathematics; there is ample opportunity to analyze more complex examples and phenomena in future studies.
The choice of topics in the book was governed by the following principles:
1. The mathematics involved should be simple, accessible to a student with no experience beyond elementary high school algebra, and explainable within a couple of pages.
Next page







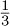 = 0.333333, but the fact that any repeating decimal, say, 0.765765765, can be easily written as a fraction of two integers follows from the formula for the geometric series. The same formula lies in the foundation of Zenos paradox of Achilles and a tortoise, covered in under a parabolic arc. Why should we care? If understanding history is a good enough reason, we can recall that by some accounts, Archimedes also took part in the defense of his town of Syracuse during the siege by the Romans (214-212 BC), and might have used his computation to design a parabolic mirror to set the enemys fleet on fire. Now, fast-forward to the twentieth century. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension was the title of the article, published in Science in 1967 by the French-American mathematician Benoit Mandelbrot, that opened a new area of study fractal geometry. The answer to the question in the title depends on how closely we look, and the closer we look, the greater the coasts length becomes. The same is true for many fractal curves that are easy to describe in words but impossible to draw precisely. One of the central tools used to understand these objects is the geometric series.
= 0.333333, but the fact that any repeating decimal, say, 0.765765765, can be easily written as a fraction of two integers follows from the formula for the geometric series. The same formula lies in the foundation of Zenos paradox of Achilles and a tortoise, covered in under a parabolic arc. Why should we care? If understanding history is a good enough reason, we can recall that by some accounts, Archimedes also took part in the defense of his town of Syracuse during the siege by the Romans (214-212 BC), and might have used his computation to design a parabolic mirror to set the enemys fleet on fire. Now, fast-forward to the twentieth century. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension was the title of the article, published in Science in 1967 by the French-American mathematician Benoit Mandelbrot, that opened a new area of study fractal geometry. The answer to the question in the title depends on how closely we look, and the closer we look, the greater the coasts length becomes. The same is true for many fractal curves that are easy to describe in words but impossible to draw precisely. One of the central tools used to understand these objects is the geometric series.