Ton J. Cleophas - Machine Learning in Medicine - a Complete Overview

Machine Learning in Medicine - a Complete Overview — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Machine Learning in Medicine - a Complete Overview" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...132

Part I
Cluster and Classification Models

Springer International Publishing Switzerland 2015

Ton J. Cleophas and Aeilko H. Zwinderman Machine Learning in Medicine - a Complete Overview 10.1007/978-3-319-15195-3_1

1. Hierarchical Clustering and K-Means Clustering to Identify Subgroups in Surveys (50 Patients)

Ton J. Cleophas 1 and Aeilko H. Zwinderman 2

(1)

Department Medicine, Albert Schweitzer Hospital, Sliedrecht, The Netherlands

(2)

Department Biostatistics and Epidemiology, Academic Medical Center, Amsterdam, The Netherlands

This chapter was previously published in Machine learning in medicine-cookbook 1 as Chap. 1, 2013.

General Purpose

Clusters are subgroups in a survey estimated by the distances between the values needed to connect the patients, otherwise called cases. It is an important methodology in explorative data mining.

Specific Scientific Question

In a survey of patients with mental depression of different ages and depression scores, how do different clustering methods perform in identifying so far unobserved subgroups.

20,00	8,00
21,00	7,00
23,00	9,00
24,00	10,00
25,00	8,00
26,00	9,00
27,00	7,00
28,00	8,00
24,00	9,00
32,00	9,00
30,00	1,00
40,00	2,00
50,00	3,00
60,00	1,00
70,00	2,00
76,00	3,00
65,00	2,00
54,00	3,00

Var 1 age

Var 2 depression score (0=very mild, 10=severest)

Var 3 patient number (called cases here)

Only the first 18 patients are given, the entire data file is entitled hierk-meansdensity and is in extras.springer.com.

Hierarchical Cluster Analysis

SPSS 19.0 will be used for data analysis. Start by opening the data file.

Command:

• Analyze.Classify.Hierarchical Cluster Analysis.enter variables.Label Case by: case variable with the values 1-50.Plots: mark Dendrogram.Method
• .Cluster Method: Between-group linkage.Measure: Squared Euclidean Distance.Save: click Single solution.Number of clusters: enter 3.Continue .OK.

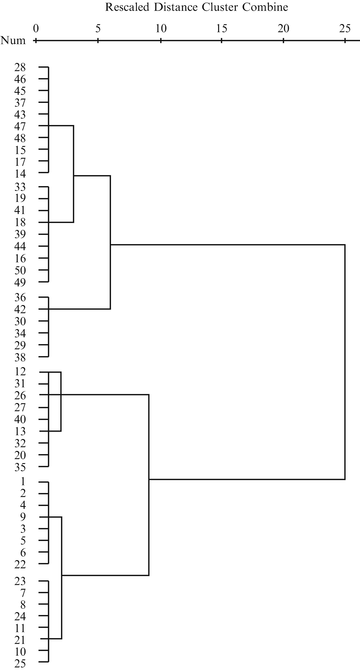
In the output a dendrogram of the results is given. The actual distances between the cases are rescaled to fall into a range of 025 units (0=minimal distance, 25=maximal distance). The cases no. 111, 2125 are clustered together in cluster 1, the cases 12, 13, 20, 26, 27, 31, 32, 35, 40 in cluster 2, both at a rescaled distance from 0 at approximately 3 units, the remainder of the cases is clustered at approximately 6 units. And so, as requested, three clusters have been identified with cases more similar to one another than to the other clusters. When minimizing the output, the data file comes up and it now shows the cluster membership of each case. We will use SPSS again to draw a Dotter graph of the data.

Command:

• Analyze.Graphs.Legacy Dialogs: click Simple Scatter.Define.Y-axis:
• enter Depression Score.X-axis: enter Age.OK.

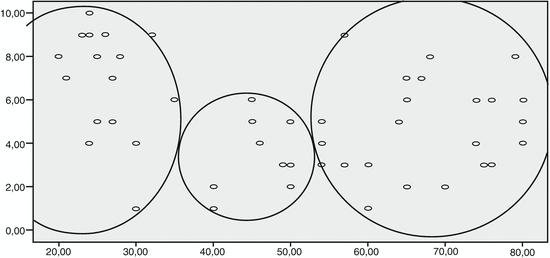
The graph (with age on the x-axis and severity score on the y-axis) produced by SPSS shows the cases. Using Microsofts drawing commands we can encircle the clusters as identified. All of them are oval and even, approximately, round, because variables have similar scales, but they are different in size.

K-Means Cluster Analysis

Command:

• Analyze.Classify.K-means Cluster Analysis.Variables: enter Age and Depression score.Label Cases by: patient number as a string variable.Number of clusters: 3 (in our example chosen for comparison with the above method).click Method: mark Iterate.click Iterate: Maximal Iterations: mark 10.Convergence criterion: mark 0.click Continue.click Save: mark Cluster Membership.click Continue.click Options: mark Initiate cluster centers.mark ANOVA table.mark Cluster information for each case.click Continue.OK.

The output shows that the three clusters identified by the k-means cluster model were significantly different from one another both by testing the y-axis (depression score) and the x-axis variable (age). When minimizing the output sheets, the data file comes up and shows the cluster membership of the three clusters.

ANOVA
Cluster	Error
Mean square	df	Mean square	df	F	Sig.
Age	8712,723		31,082		280,310	,000
Depression score	39,102		4,593		8,513	,001

We will use SPSS again to draw a Dotter graph of the data.

Command:

• Analyze.Graphs.Legacy Dialogs: click Simple Scatter.Define.Y-axis: enter Depression Score.X-axis: enter Age.OK.

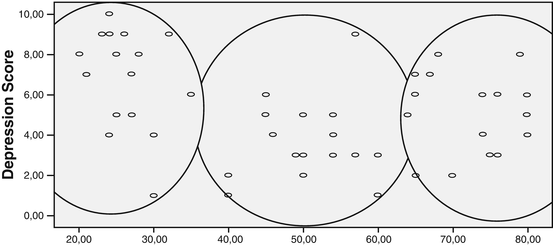
The graph (with age on the x-axis and severity score on the y-axis) produced by SPSS shows the cases. Using Microsofts drawing commands we can encircle the clusters as identified. All of them are oval and even approximately round because variables have similar scales, and they are approximately equal in size.

Conclusion

Clusters are estimated by the distances between the values needed to connect the cases. It is an important methodology in explorative data mining. Hierarchical clustering is adequate if subgroups are expected to be different in size, k-means clustering if approximately similar in size. Density-based clustering is more appropriate if small outlier groups between otherwise homogenous populations are expected. The latter method is in Chap..

Note

More background, theoretical and mathematical information of the two methods is given in Machine learning in medicine part two, Chap. 8 Two-dimensional Clustering, pp 6575, Springer Heidelberg Germany 2013. Density-based clustering will be reviewed in the next chapter.

Next page

1234567...132

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Machine Learning in Medicine - a Complete Overview»

Look at similar books to Machine Learning in Medicine - a Complete Overview. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Steven Cooper

Machine Learning for Beginners: An Introduction for Beginners, Why Machine Learning Matters Today and How Machine Learning Networks, Algorithms, Concepts and Neural Networks Really Work

HIROTO UTAGAWA

MACHINE LEARNING GLOSSARY: THE BEGINNERS GUIDE TO MACHINE LEARNING

Subhi J. AlAref M.D. (editor)

Machine Learning in Cardiovascular Medicine

Soranson

Python Machine Learning: The Complete Guide to Understand Python Machine Learning for Beginners and Artificial Intelligence

Mathur

Machine learning applications using Python: cases studies from healthcare, retail, and finance

Park

Machine Learning with Python: Complete Step-by-Step Guide for Beginners to Learning Machine Learning Technology, Principles, Application and The Importance It Has Today

Cleophas Ton J. M.

Machine Learning in Medicine

Soranson

Python Machine Learning: How to learn Machine Learning with Python. The Complete Guide to Understand Python Machine Learning for Beginners and Artificial Intelligence

Ton J. Cleophas

Machine Learning in Medicine – A Complete Overview

Ton J. Cleophas

SPSS for Starters and 2nd Levelers

Ton J. Cleophas

Clinical Data Analysis on a Pocket Calculator

Ton J. Cleophas

Statistical Analysis of Clinical Data on a Pocket Calculator

Discussion, reviews of the book Machine Learning in Medicine - a Complete Overview and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.