1.1 Concept
The Finite Element Analysis (FEA) method, originally introduced by Turner et al. (1956), is a powerful computational technique for approximate solutions to a variety of real-world engineering problems having complex domains subjected to general boundary conditions. FEA has become an essential step in the design or modeling of a physical phenomenon in various engineering disciplines. A physical phenomenon usually occurs in a continuum of matter (solid, liquid, or gas) involving several field variables. The field variables vary from point to point, thus possessing an infinite number of solutions in the domain. Within the scope of this book, a continuum with a known boundary is called a domain.
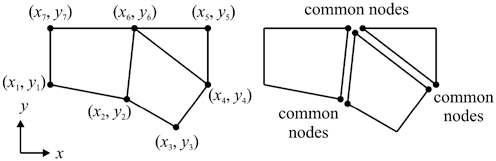
The basis of FEA relies on the decomposition of the domain into a finite number of subdomains (elements) for which the systematic approximate solution is constructed by applying the variational or weighted residual methods. In effect, FEA reduces the problem to that of a finite number of unknowns by dividing the domain into elements and by expressing the unknown field variable in terms of the assumed approximating functions within each element. These functions (also called interpolation functions ) are defined in terms of the values of the field variables at specific points, referred to as nodes. Nodes are usually located along the element boundaries, and they connect adjacent elements.
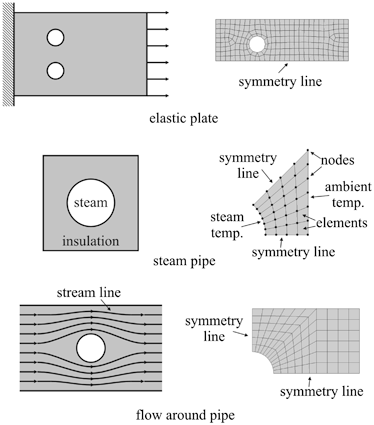
The ability to discretize the irregular domains with finite elements makes the method a valuable and practical analysis tool for the solution of boundary, initial, and eigenvalue problems arising in various engineering disciplines. Since its inception, many technical papers and books have appeared on the development and application of FEA. The books by Desai and Abel (1971), Oden (1972), Gallagher (1975), Huebner (1975), Bathe and Wilson (1976), Ziekiewicz (1977), Cook (1981), and Bathe (1996) have influenced the current state of FEA. Representative common engineering problems and their corresponding FEA discretizations are illustrated in Fig..
Fig. 1.1
FEA representation of practical engineering problems
The finite element analysis method requires the following major steps:
Discretization of the domain into a finite number of subdomains (elements).
Selection of interpolation functions.
Development of the element matrix for the subdomain (element).
Assembly of the element matrices for each subdomain to obtain the global matrix for the entire domain.
Imposition of the boundary conditions .
Solution of equations.
Additional computations (if desired).
There are three main approaches to constructing an approximate solution based on the concept of FEA:
Direct Approach
This approach is used for relatively simple problems, and it usually serves as a means to explain the concept of FEA and its important steps (discussed in Sect. ).
Weighted Residuals
This is a versatile method, allowing the application of FEA to problems whose functionals cannot be constructed. This approach directly utilizes the governing differential equations, such as those of heat transfer and fluid mechanics (discussed in Sect. ).
Variational Approach
This approach relies on the calculus of variations, which involves extremizing a functional. This functional corresponds to the potential energy in structural mechanics (discussed in Sect. ).
In matrix notation, the global system of equations can be cast into
where
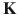
is the system stiffness matrix ,
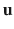
is the vector of unknowns , and
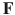
is the force vector. Depending on the nature of the problem,
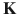
may be dependent on
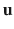
, i.e.,
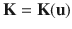
and
may be time dependent, i.e.,
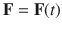













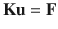
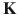 is the system stiffness matrix ,
is the system stiffness matrix , 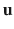 is the vector of unknowns , and
is the vector of unknowns , and 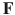 is the force vector. Depending on the nature of the problem,
is the force vector. Depending on the nature of the problem, 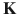 may be dependent on
may be dependent on 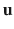 , i.e.,
, i.e., 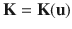 and
and 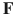 may be time dependent, i.e.,
may be time dependent, i.e.,