Wiśniewski - Prototyping of Concurrent Control Systems Implemented in FPGA Devices

Prototyping of Concurrent Control Systems Implemented in FPGA Devices — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Prototyping of Concurrent Control Systems Implemented in FPGA Devices" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...69

Springer International Publishing Switzerland 2017

Remigiusz Winiewski Prototyping of Concurrent Control Systems Implemented in FPGA Devices Advances in Industrial Control 10.1007/978-3-319-45811-3_1

1. Introduction

Remigiusz Winiewski 1

(1)

Faculty of Computer, Electrical and Control Engineering, Institute of Electrical Engineering, University of Zielona Gra, Zielona Gra, Poland

Remigiusz Winiewski

Email:

1.1 Context and Motivation

Control systems surround us everywhere. They can be found in almost all areas of human life, such as medical care [].

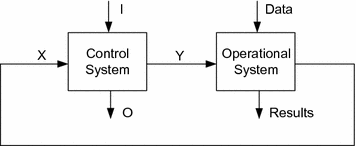
Formally, a control system is a system, that is responsible for control and management of another system (often called as an operational system ) [.

In the sequential control systems , the subsequent sets of operations for the operational system are computed and generated in a sequence . For example, a central processor unit (CPU) operates in this way, managing instructions to be handled [].

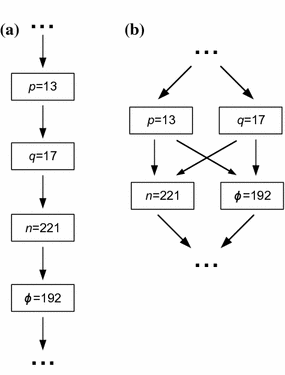
Let us demonstrate the idea of sequential computation. An RSA algorithm is one of the most popular public-key cryptosystems [a presents a pseudo flowchart, where particular instructions are performed sequentially. Initially, the first prime ( p ) is loaded (read) to the the control system. Analogically, the second prime ( q ) is loaded when the previous instruction is completed. Furthermore, the product of two primes is obtained. In the fourth step, the Euler totient function is calculated. Please note, that we just show the idea of sequential computation, thus all the presented actions are simplified and treated as a single instruction.

Fig. 1.1

Model of the control and operational systems

Fig. 1.2

An idea of a sequential and b concurrent computation

A concurrent control system can be seen as an extension of a sequential control system. The sets of operations for the operational system (or systems) may be computed and generated either sequentially or concurrently .

Figure b shows the idea of concurrent computation. In the presented example, both primes used in the RSA algorithm are read at the same time. Furthermore, the computation of their product, as well as calculation of the Euler totient function is performed simultaneously. Of course, proper synchronization between particular actions ought to be assured. For example, the computation of the product of the primes should be done only if both numbers have been loaded to the concurrent control system. Since synchronization is a very important aspect of prototyping of concurrent control systems, we will discuss it in more detail later.

Generally, a concurrent system is composed of the set of processes (components) that are executed at the same time. Each of them usually performs a particular task (or tasks). Such a situation is mostly known from the concurrent programming [].

In case of digital devices, a concurrent control system is often formally specified by a Petri net . This mathematical tool permits for easy and comfortable description of the prototyped design. First proposed in [].

Very often (but not always) prototyping of concurrent controllers specified by a Petri net involves splitting of the system into separate subsystems [].

The commonly used decomposition methods of concurrent control systems base on a linear algebra (place invariants analysis) [].

Beside the decomposition of the system, linear algebra is mainly used in the analysis of the concurrent controller described by a Petri net []. Furthermore, concurrency and sequentiality relations can be checked. Those relations are especially useful in the selection of concurrent (or sequential) areas of the system.

Similarly to the decomposition, the main bottleneck of the analysis is exponential number of states that may occur in the design. Therefore, very often additional methods are applied prior to the main analysis of the system. For example, reduction techniques simplify the initial Petri net [].

From the prototyping point of view, concurrent control systems can be divided into two main groups:

• Distributed concurrent control systems , generally implemented in more than one device. For example, it can be a set of connected Programmable Logic Controllers (PLCs), each of devices performs a sequential task [].
• Integrated concurrent control systems , generally implemented in a single device, that supports concurrency (for example, digital circuits such as Application Specific Integrated Circuits (ASICs) []). Since the controller is implemented in a single device, its modules usually share the same clock signal, thus the synchronization between them is much easier than in case of distributed systems.

Various synchronization techniques of concurrent systems can be found in the literature. Among others, the general synchronization concepts are presented in [].

Integrated concurrent control systems are often oriented on the implementation in the programmable device. Especially Field Programmable Gate Arrays (FPGAs) are considered. High performance, flexibility, and configurability resulted in their application in various aspects of human life, such as medicine [].

Latest FPGA devices, apart from the traditional static configuration of the entire system, offer much more sophisticated mechanisms. Partial reconfiguration allows replacement of selected parts of the system, without having to reprogram the entire structure of the FPGA [].

Summarizing the above presented discussion, it can be stated that there are gaps in the existing methods of decomposition, analysis, and prototyping of concurrent control systems. Looking in more detail, two major aspects can be noticed:

• The main bottleneck of the decomposition and analysis of a concurrent control system specified by a Petri net is computational complexity of algorithms. In most cases such complexity is exponential, which means that the solution may never be found. Thus, the existing methods balance between optimal results and reasonable computational time.
• There is a lack of a dedicated prototyping flow of concurrent control systems specified by a Petri net intended for implementation in an FPGA and further partial reconfiguration of the design.

The aim of the book is to introduce concurrent control systems and to discuss solutions of effective prototyping, analysis, and decomposition of such systems . In the book, classical approaches based on linear algebra, as well as novel algorithms (with application of perfect graphs or hypergraphs) are analyzed and discussed in detail. Especially, the presented decomposition method based on the perfect graphs theory (Chaps. ).

The main purpose of the book is to present prototyping methods of concurrent control systems, intended for implementation in FPGAs with a possibility of further partial reconfiguration of the controller . A concurrent system is represented by an interpreted Petri net , which naturally reflects concurrent and sequential relationships of a modelled controller. Furthermore, the system is decomposed into sequential components. Three alternative decomposition methods are presented in the book (Chap. ).

Finally, the complete prototyping flow of a concurrent control system intended for implementation in the FPGA with a possibility of further partial reconfiguration is proposed. Two different approaches are introduced. The first one is dedicated for the static partial reconfiguration of the design, while the second focuses on the dynamic partial reconfiguration of the concurrent control system (Chaps. ).

Next page

1234567...69

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Prototyping of Concurrent Control Systems Implemented in FPGA Devices»

Look at similar books to Prototyping of Concurrent Control Systems Implemented in FPGA Devices. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Józef Korbicz (editor)

Advances in Diagnostics of Processes and Systems: Selected Papers from the 14th International Conference on Diagnostics of Processes and Systems ... in Systems, Decision and Control, 313)

Posch

Hands-on embedded programming with C++ 17: create versatile and robust embedded solutions for MCUs and RTOSes with modern C++

Vijay Nath

Nanoelectronics, Circuits and Communication Systems: Proceeding of NCCS 2019

Soshin

Hands-on design patterns with Kotlin build scalable applications using traditional, reactive, and concurrent design patterns in Kotlin

Prokopec

Learning concurrent programming in Scala: learn the art of building intricate, modern, scalable, and concurrent applications using Scala

Douglas C. Schmidt

Pattern-Oriented Software Architecture, Patterns for Concurrent and Networked Objects

Dr. Rian Quinn

Hands-On System Programming with C++: Build performant and concurrent Unix and Linux systems with C++17

Julio Sanchez

Embedded Systems Circuits and Programming

Badr Benmammar

Concurrent, Real-Time and Distributed Programming in Java: Threads, RTSJ and RMI

Cem Unsalan

Digital System Design with FPGA: Implementation Using Verilog and VHDL

Elliot Forbes

Learning Concurrency in Python

Leonardo Borges

Clojure Reactive Programming

Discussion, reviews of the book Prototyping of Concurrent Control Systems Implemented in FPGA Devices and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.