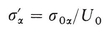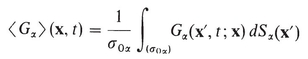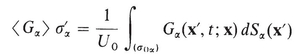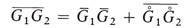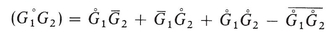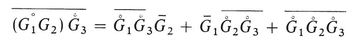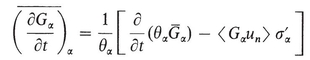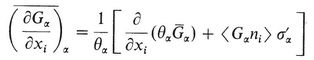Consider the domain ( U 0) of volume U 0 which is a Representative Elementary Volume of a porous medium comprised of several phases . Each phase occupies a volume U 0 within U 0; its volumetric fraction is
For any tensorial field G (x, t ), the spatial average (x, t ) of G at time t and point x, over the domain ( U 0) c ( U 0) centered at x is defined by
The average is also called intrinsic phase average of G in U 0. The quantity
is the deviation of G at a point x inside U 0 (centered at x) from its average over U 0. Also
The space x is the macroscopic space , whereas x is the microscopic space . From (A-1) and (A-2), it follows that
is another average, called the phase average of G in U 0. It is the macroscopic value of G in the phase.
As an example, let G V be the microscopic velocity vector in the phase. Then 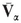 is the average velocity of the phase
is the average velocity of the phase
is the macroscopic velocity field of (recall that V = 0 outside U 0).
A-2 SPECIFIC DISCHARGE
Let P(x) be a point in a multiphase porous medium domain through which flow takes place. Similar to the definition of a Representative Elementary Volume (Sec. 2-5), we may also define at every point x a Representative Elementary Area
(REA) A 0, such that an average of a property over it will represent a meaningful value of that property at its centroid. The area A 0 j () A 0 j at P is facing the direction Ij.
In order to interpret the meaning of the product 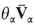 at point P(x), let U 0 have the shape of a straight cylinder having a cross-sectional area A 0 j facing the direction 1j and length L j . Let V j be the component in the direction 1j of the local velocity at all points in the phase, that is, V j = 0 outside the phase. Then, from (A-7)
at point P(x), let U 0 have the shape of a straight cylinder having a cross-sectional area A 0 j facing the direction 1j and length L j . Let V j be the component in the direction 1j of the local velocity at all points in the phase, that is, V j = 0 outside the phase. Then, from (A-7)
Now, the expression in the square brackets in (A-8) is the specific discharge 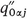 , that is, the total discharge per unit area of A 0 j
, that is, the total discharge per unit area of A 0 j
so that 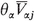 is the average of
is the average of 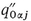 over parallel cross-sectional areas of the REV (here from x - ( L j l2 ) 1j to x + ( L j /2) 1j). For the sake of simplicity, we have assumed that the REV has a cylindrical shape, with U 0 = L j A 0 j .
over parallel cross-sectional areas of the REV (here from x - ( L j l2 ) 1j to x + ( L j /2) 1j). For the sake of simplicity, we have assumed that the REV has a cylindrical shape, with U 0 = L j A 0 j .
We have thus shown that the macroscopic velocity 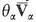 defined by (A-7) has the meaning of the specific discharge vector q of the phase at that point. It is of interest to note that q is a function of (x, t ) only, independent of the direction chosen for Ij.
defined by (A-7) has the meaning of the specific discharge vector q of the phase at that point. It is of interest to note that q is a function of (x, t ) only, independent of the direction chosen for Ij.
A-3 SOME AVERAGING RULES (BACHMAT, 1972; GRAY AND LEE, 1977)
( a ) Let 0 denote the total surface area between the phase and the other phases within U 0. We define the specific surface of the phase by
and the average of G (x, t ) over 0 for a given ( U 0) by
Also
(b) Average of a product
Also
Hence
(c) Average of a time derivative
where u n is the speed of displacement, along the outward normal, of a point on the interface between the phase and the other phases within U 0. Cases of interest:
1. G 1. Then = land
/ t = U n
2. U n = 0, that is, the configuration of the phase is nondeformable. Then
( G / t ) = / t
(d) Average of a spatial derivative
where n i is the i -component of a unit vector normal to and pointing outwards.
In (A-16) we have to consider only the multiply connected portion of the domain.
Case of special interest:














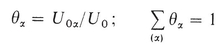
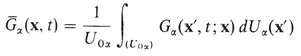
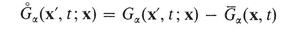
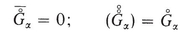
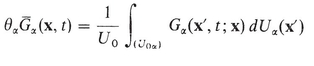
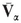 is the average velocity of the phase
is the average velocity of the phase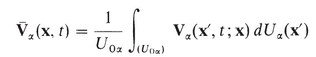
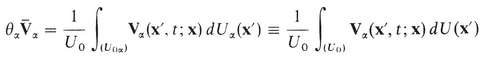
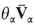 at point P(x), let U 0 have the shape of a straight cylinder having a cross-sectional area A 0 j facing the direction 1j and length L j . Let V j be the component in the direction 1j of the local velocity at all points in the phase, that is, V j = 0 outside the phase. Then, from (A-7)
at point P(x), let U 0 have the shape of a straight cylinder having a cross-sectional area A 0 j facing the direction 1j and length L j . Let V j be the component in the direction 1j of the local velocity at all points in the phase, that is, V j = 0 outside the phase. Then, from (A-7)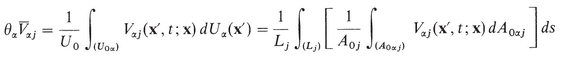
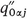 , that is, the total discharge per unit area of A 0 j
, that is, the total discharge per unit area of A 0 j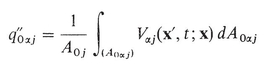
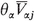 is the average of
is the average of 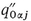 over parallel cross-sectional areas of the REV (here from x - ( L j l2 ) 1j to x + ( L j /2) 1j). For the sake of simplicity, we have assumed that the REV has a cylindrical shape, with U 0 = L j A 0 j .
over parallel cross-sectional areas of the REV (here from x - ( L j l2 ) 1j to x + ( L j /2) 1j). For the sake of simplicity, we have assumed that the REV has a cylindrical shape, with U 0 = L j A 0 j .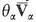 defined by (A-7) has the meaning of the specific discharge vector q of the phase at that point. It is of interest to note that q is a function of (x, t ) only, independent of the direction chosen for Ij.
defined by (A-7) has the meaning of the specific discharge vector q of the phase at that point. It is of interest to note that q is a function of (x, t ) only, independent of the direction chosen for Ij.