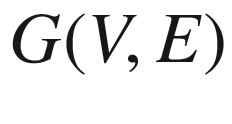Krishna Raj P.M. - Practical Social Network Analysis with Python

The Computer Communications and Networks series is a range of textbooks, monographs and handbooks. It sets out to provide students, researchers, and non-specialists alike with a sure grounding in current knowledge, together with comprehensible access to the latest developments in computer communications and networking.

Emphasis is placed on clear and explanatory styles that support a tutorial approach, so that even the most complex of topics is presented in a lucid and intelligible manner.

More information about this series at http://www.springer.com/series/4198

Additional material to this book can be downloaded from http://extras.springer.com .

This Springer imprint is published by the registered company Springer Nature Switzerland AG

The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland

Although there are innumerable complex systems and therefore such a large number of networks, the focus of this book is social networks . A social network contains individuals as nodes and links representing the relationship between these individuals. The study of social networks is of particular interest because it focuses on this abstract view of human relationships which gives insight into various kinds of social relationships ranging all the way from bargaining power to psychological health.

We describe in detail graph theory, statistical properties and graph algorithms. Through this, we hope to describe the various patterns and statistical properties of networks, introduce design principles and models for looking at these properties, provide an understanding as to why networks are organized the way they are and apply our understanding to predict behaviour of networks.

The world around us provides a plethora of instances of complex systems . Transportation networks, social media applications, proteinprotein interactions, auction houses, spreading of diseases and so on are all examples of complex systems we all encounter in our daily lives. All of these systems are extremely complicated to comprehend because they contain several seemingly disparate components which may be directly or indirectly related to one another. These components exhibit behaviour which is increasingly difficult to reason about and too risky to tinker with. Even a slight seemingly innocuous change in one of the components can have a domino effect which could have unexpected consequences.

Figure depicts the Internet on a global scale. This figure can help paint a sort of picture as to how complicated a system really is, and how one must proceed in order to understand such a complex system.

Fig. 1

Illustration of the global Internet. Online at https://www.weforum.org/projects/internet-for-all

Each of these complex systems (especially the Internet) has its own unique idiosyncrasies but all of them share a particular commonality in the fact that they can be described by an intricate wiring diagram, a network , which defines the interactions between the components. We can never fully understand the system unless we gain a full understanding of its network.

Network

A network is a collection of objects where some pairs of these objects are connected by links. These objects are also sometimes referred to as nodes. By representing a complex system through its network, we are able to better visualize the system and observe the interconnections among the various nodes. From close examination of networks, we can gather information about which nodes are closely linked to one another, which are sparsely linked, whether there is a concentration of links in a particular part of the network, do some nodes have a very high number of links when compared to others and so on.

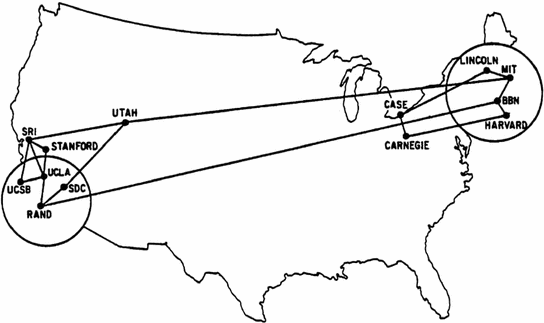
Figure illustrates network corresponding to the ARPANET in December 1970 (what the Internet was called then). It consisted of 13 sites where the nodes represent computing hosts and links represent direct communication lines between these hosts.

Fig. 2

ARPANET in December 1970. Computing hosts are represented as nodes and links denote the communication lines. Online at https://imgur.com/gallery/Xk9MP

Graph

Several properties can be retrieved from these networks but there are some others which require a more mathematical approach. In the purview of mathematics, networks in its current state fail to be amenable. To allow for this amenability, a network is represented as a graph . In this view, a graph can be described as a mathematical representation of networks which acts as a framework for reasoning about numerous concepts. More formally, a graph can be defined as