Paul Miller - An Introductory Course in Computational Neuroscience

Computational Neuroscience

Terrence J. Sejnowski and Tomaso. A Poggio, editors

For a complete list of books in this series, see the back of the book and https://mitpress.mit.edu/books/series/computational-neuroscience

An Introductory Course in Computational Neuroscience

Paul Miller

The MIT Press

Cambridge, Massachusetts

London, England

2018 Massachusetts Institute of Technology

All rights reserved No part of this book may be reproduced in any form by any electronic or mechanical means (including photocopying, recording, or information storage and retrieval) without permission in writing from the publisher.

This book was set in Times by Toppan Best-set Premedia Limited Printed and bound in the United States of America.

Library of Congress Cataloging-in-Publication Data

Names: Miller, Paul, 1969- author.

Title: An introductory course in computational neuroscience / Paul Miller.

Description: Cambridge, MA : The MIT Press, 2018. | Series: Computational

neuroscience series | Includes bibliographical references and index.

Identifiers: LCCN 2018003118 | ISBN 9780262038256 (hardcover : alk. paper)

eISBN 9780262347556

Subjects: LCSH: Computational neuroscience--Textbooks. |

Neurosciences--Mathematics.

Classification: LCC QP357.5 .M55 2018 | DDC 612.8/233--dc23 LC record available at https://lccn.loc.gov/2018003118

ePub Version 1.0

Computational neuroscience is an approach to understanding the development and function of nervous systems at many different structural scales, including the biophysical, the circuit, and the systems levels. Methods include theoretical analysis and modeling of neurons, networks, and brain systems and are complementary to empirical techniques in neuroscience. Areas and topics of particular interest to this book series include computational mechanisms in neurons, analysis of signal processing in neural circuits, representation of sensory information, systems models of sensorimotor integration, computational approaches to biological motor control, and models of learning and memory. Further topics of interest include the intersection of computational neuroscience with engineering, from representation and dynamics, to observation and control.

Terrence J. Sejnowski

Tomaso Poggio

I am grateful to the following people for their constructive comments and suggestions, which helped improve this book: Jonathan Cannon, Irv Epstein, John Ksander, Stephen Lovatt, Eve Marder, Alexandra Miller, Candace Miller, Ray Morin, Narendra Muckerjee, Alireza Soltani, Stephen Van Hooser, Ryan Young; and the following members of the Brandeis University Computational Neuroscience Classes (Spring 2017 and Spring 2018): Taniz Abid, Rabia Anjum, Apoorva Arora, Sam Aviles, Remi Boros, Brian Cary, Kieran Cooper, Ron Gadot, Sophie Grutzner, Noah Guzman, Lily He, Dahlia Kushinsky, Jasmine Quynh Le, Andrew Lipnick, Cherubin Manokaran, Sigal Sax, Nathan Schneider, Daniel Shin, Elizabeth Tilden, David Tresner-Kirsch, Nick Trojanowski, Vardges Tserunyan, and Jeffrey Zhu.

Several tutorials in this book evolved from course materials produced by Larry Abbott, Tim Vogels, and Xiao-Jing Wang, to whom I am grateful for introducing me to neuroscience.

I am particularly thankful to Candace Miller for her encouragement during this enterprise and to Brandeis University for its support.

I designed this book to help beginning students access the exciting and blossoming field of computational neuroscience and lead them to the point where they can understand, simulate, and analyze the quite complex behaviors of individual neurons and brain circuits. I was motivated to write the book when progressing to the flipped or inverted classroom approach to teaching, in which much of the time in the classroom is spent assisting students with the computer tutorials while the majority of information-delivery is via students reading the material outside of class. To facilitate this process, I assume less mathematical background of the reader than is required for many similar texts (I confine calculus-based proofs to appendices) and intersperse the text with computer tutorials that can be used in (or outside of) class. Many of the topics are discussed in more depth in the book Theoretical Neuroscience by Peter Dayan and Larry Abbott, the book I used to learn theoretical neuroscience and which I recommend for students with a strong mathematical background.

The majority of figures, as well as the tutorials, have associated computer codes available online, at github, https://github.com/primon23/Intro-Comp-Neuro, at my website, http://people.brandeis.edu/~pmiller, and at the website of MIT Press, https://mitpress.mit.edu/computationalneuroscience. I hope these codes may be a useful resource for anyone teaching or wishing to further their understanding of neural systems.

When using this book for a course without prerequisites in calculus or computer coding, the first two weeks of the course (at a minimum) should be spent covering the preliminary material found in chapter 1. The contents of the different sections of this chapter are introduced here.

In my experience, many students who enjoy solving mathematical or computational problems take a course such as computational neuroscience as their first introduction to neuroscience, or even as their first university-level course in the life sciences. For such students, section 1.2 offers a very basic summary of the meaning and relevance of biological and neurological terms that are used but not introduced elsewhere in the book. The newcomer to neuroscience should read section 1.2 before commencing the course.

The ability of neurons to convey and process information depends on their electrical properties, in particular the spatial and temporal characteristics of the potential difference across the neurons membraneits membrane potential. Nearly all of single neuron modeling revolves around calculating the causes and effects of changes in the membrane potential. To understand fully the relevant chapters in this book, it is first necessary for the reader to appreciate some of the underlying physics, so a background is provided in section 1.3 of this chapter.

Membrane potential,

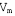
The potential difference across the membrane of a cell, which is highly variable in neurons, ranging over a scale of tens of millivolts.

The universe runs on differential equations, thanks to the continuity of space and time. The same applies to the brain, so at the heart of this computational modeling course is the requirement to write computer codes that solve differential equations. This may sound daunting, but it is in fact a lot easier than solving the same differential equations by the analytical methods one might find in a mathematics course. As a preliminary to delving into the various specific ordinary differential equations that we will find in this course, it is first important to understand what an ordinary differential equation is and what it means.

A property of the system that changes with time.

A property of the system that is fixed during an experiment or simulation.