Mark Ladd and Rex Palmer Structure Determination by X-ray Crystallography 5th ed. 2013 Analysis by X-rays and Neutrons 10.1007/978-1-4614-3954-7_1 Springer Science+Business Media New York 2013
1. Crystal Morphology and Crystal Symmetry
1.1 Brief Historical Introduction
Crystals, with their plane faces, sharp angles, and color, have excited interest since the earliest times. Their color and decorative qualities are recorded in the Bible []: we need not start as far back as that, but will consider instead some of the highlights in the build-up of the science of Crystallography.
The Swiss naturalist Conrad Gessner [] published his work on the Iceland Spar modification of calcium carbonate: he measured the interfacial angles (q.v.) of crystal fragments and found that the (cleavage) fragments have the same shape as the original crystal.
Fig. 1.1
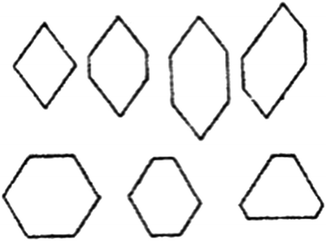
Examples of Stenos drawings of transverse sections of different crystal specimens of quartz, SiO2; the interfacial angles are 120 or (120/2) in each case
Johannes Kepler, best known for his research in astronomy, worked sometime for Emperor Rudolph II of Austria, who was somewhat negligent in paying salaries. Kepler, who was without money with which to purchase a Christmas present for a friend in 1611, wrote a booklet entitled The Six-Cornered Snowflake [. He had noticed that snow crystals of whatever shape always exhibited sixfold symmetry. He speculated on a relationship between the snow crystal and a hexagonal close packing of spheres: he recognized the genre of crystal symmetry, which was to be developed about two centuries years later. Jokingly, he passed off his New Years Gift as a mere nothing (like his finances), making a play on the word nix , which means snowflake in Latin but nothing in Lower German, Keplers language.
Fig. 1.2
The cover (in translation) of Keplers booklet on The Six-Cornered Snowflake ; some of Keplers many drawings of snowflakes appear on the cover (reproduced by courtesy of Paul Dry Books)
Over the period 16881705, many investigations by the Italian physicist Giovanni Guglielmini [], for measuring interfacial angles on crystals.
His compatriot Ren Just (Abb) Hay [ illustrates some of Hays figures. He laid the foundation for the law of rational intercepts (q.v.), which demonstrated, albeit implicitly, a shape for the unit cell (q.v.) of a crystal. He described also different crystal shapes, or habits , obtained by the packing of different shaped blocks.
Fig. 1.3
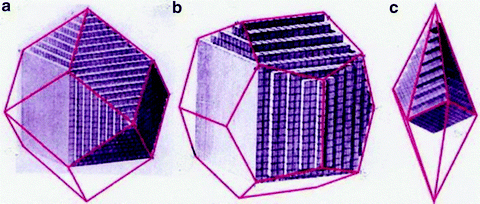
Examples of Hays figures. ( a ) Rhombic dodecahedron formed from stacked cubes, as in garnet (idealized formula Ca3Al2Si3O12). ( b ) Pentagonal dodecahedron formed from stacked cubes, as in K2Mn2(SO4)3. ( c ) Scalenohedron formed from stacked rhombohedra, as in calcite, CaCO3
In the period 18041815, the German scientists Christian Weiss [ illustrates two examples of crystal class.
Fig. 1.4
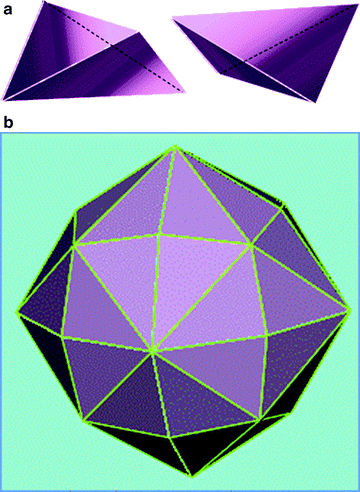
Examples of crystal classes: ( a ) Rhombic disphenoid, showing left-hand and right-hand enantiomorphs (q.v.). ( b ) Hex(akis)octahedron
A next landmark was that contained in the work of William Miller, 1839, who proposed an unambiguous notation for specifying the orientations of the faces of a crystal, leading to the Miller Indices [] (q.v.), based on the scalar equation of a plane; the law of rational indices is clear from Millers workthe descriptor law of rational ratios of intercepts is perhaps more apt.
The regular arrangements of points in space were addressed by August Bravais [] in 1846, who derived the 14 Bravais lattices. Actually, Frankenheim had derived 15 such lattices in 1842, but Bravais showed that two of them were identical. For his infelicity, Frankenheims name is frequently omitted from a discussion of lattices, albeit the nature of his 15th lattice was never completely clear.
Continuing the development of crystal symmetry, we have at the end of the nineteenth century, Yevgraf Fyodorov [] (in Britain), all independently, describing the 230 ordered spatial patterns, or space groups (q.v.), that represented the possible ways of arranging infinite arrays of points (atoms) regularly in space, commensurate with the 14 Bravais lattices.
By that time, the work of mineralogists and mathematicians had led to a well-defined study of the external form (morphology) of crystals, as well as to predictions about their internal structure. The totality of mineralogical studies was collected in the extensive six-volume treatise ChemischeKristallographie of Paul von Groth, the first part of which was published in 1904. The time was right for a major breakthrough, and we arrive at the year 1912 and the inception of the study of crystals by X-ray diffraction methods: X-ray Crystallography was born.
The classic experiment [ shows X-ray diffraction patterns from early experiments on X-ray diffraction.
Fig. 1.5
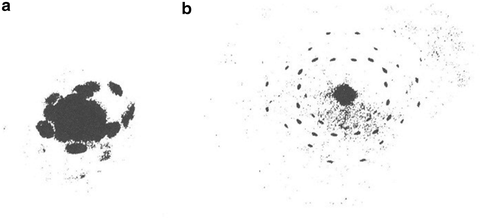
The first X-ray diffraction photograph by Friedrich et al. []. ( a ) Copper sulfate pentahydrate, CuSO45H2O, showing no symmetry. ( b ) Zinc blende (the first crystal structure to be fully determined), ZnS, showing fourfold symmetry (Bragg WH, Bragg WL (1949) The crystalline state, vol 1. G. Bell and Sons)
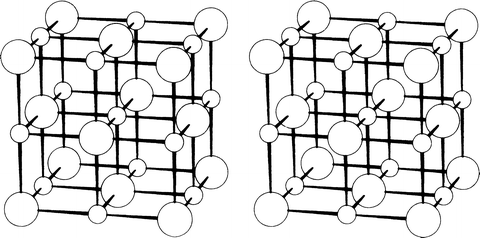
The results from this work may be said to be a landmark in the development of modern science. The diffraction technique that was initiated by Laue was improved quickly by W. L. Bragg, in his work on crystals of the alkali-metal halides and other crystals. Barlow, one of those who had derived the space groups earlier, had also developed structure models for some metallic elements, and simple binary compounds such as sodium chloride, cesium chloride, and zinc blende. None of his results was proved at that time: all were speculative, but remarkably accurate, as it turned out.
Bragg [ is a stereoview of the structure of sodium chloride, NaCl. Several stereoviews are used in this book in order to demonstrate clearly the three-dimensional nature of crystal structures, and Appendix A describes the process of stereoviewing, and the construction of a simple stereoviewer.