The book provides an in-depth look at programming in assembly language, Java, Standard ML, and Prolog. However, the programming language concepts covered in this text apply to all languages in use today. The goal of the text is to help you understand how to use the paradigms and models of computation these languages represent to solve problems. The text elaborates on when these languages may be appropriate for a problem by showing you how they can be used to implement a programming language. Many of the problems solved while implementing a programming language are similar to other problems in computer science. The text elaborates on techniques for problem solving that you may be able to apply in the future. You might be surprised by what you can do and how quickly a program can come together given the right choice of language.
1.1 Historical Perspective
Much of what we attribute to Computer Science actually came from Mathematics. Many mathematicians are programmers that have written their programs, or proofs in the words of Mathematics, using mathematical notation. In the mid 1800s abstract algebra and geometry were hot topics of research among mathematicians. In the early 1800s Niels Henrik Abel, a Norwegian mathematician, was interested in solving a problem called the quintic equation. Eventually he developed a new branch of mathematics called Group Theory with which he was able to prove there was no general algebraic solution to the quintic equation. Considering the proof of this required a new branch of mathematics, much of Abels work involved developing the mathematical notation or language to describe his work. Unfortunately, Abel died of tuberculosis at twenty six years old.
Sophus Lie ( pronounced Lee ), pictured in Fig. , was another Norwegian mathematician who lived from 18421899 [20]. He began where Abels research ended and explored the connection of Abstract Algebra and Group Theory with Geometry. From this work he developed a set of group theories, eventually named Lie Groups. From this discovery he found ways of solving Ordinary Differential Equations by exploiting properties of symmetry within the equations [8]. One Lie group, the
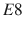
group was too complicated to map in Lies time. In fact, it wasnt until 2007 that the structure of the
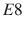
group could be mapped because the solution produced sixty times more data than the human genome project [1].
While the techniques Lie and Abel discovered were hard for people to learn and use at the time, today computer programs capable of symbolic manipulation use Lies techniques to solve these and other equally complicated problems. And, the solutions of these problems are very relevant in the world today. For example, the work of Sophus Lie is used in the design of aircraft.
As mathematicians problem solving techniques became more sophisticated and the problems they were solving became more complex, they were interested in finding automated ways of solving these problems. Charles Babbage (17911871) saw the need for a computer to do calculations that were too error-prone for humans to perform. He designed a difference engine to compute mathematical tables when he found that human computers werent very accurate [27]. However, his computer was mechanical and couldnt be built using engineering techniques known at that time. In fact it wasnt completed until 1990, but it worked just as he said it would over a hundred years earlier.
Charles Babbages difference engine was an early attempt at automating a solution to a problem, but others would follow of course. Alan Turing was a British mathematician and one of the first computer scientists. He lived from 19121954. In 1936 he wrote a paper entitled, On Computable Numbers, with an Application to the Entscheidungsproblem [23]. The Entscheidungsproblem, or decision problem, had been proposed a decade earlier by a German mathematician named David Hilbert. This problem asks: Can an algorithm be defined that decides if a statement given in first order logic can be proved from a set of axioms and known truth values? The problem was later generalized to the following question: Can we come up with a general set of steps that given any algorithm and its data, will decide if it terminates? In Alan Turings paper, he devised an abstract machine called the Turing Machine. This Turing Machine was very general and simple. It consisted of a set of states and a tape. The set of states were decided on by a programmer. The machine starts in the start state as decided by the programmer. From that state it could read a symbol from a tape. Based on the symbol it could write a symbol to the tape and move to the left or right, while transitioning to another state. As the Turing machine ran, the action that it took was dictated by the current state and the symbol on the tape. The programmer got to decide how many states were a part of the machine, what each state should do, and how to move from one state to another. In Turings paper he proved that such a machine could be used to solve any computable function and that the decision problem was not solvable by this machine. The more general statement of this problem was named the Halting Problem . This was a very important result in the field of theoretical Computer Science.
In 1939 John Atanasoff, at Iowa State University, designed what is arguably the first computer, the ABC or Atanasoff-Berry Computer [28]. Clifford Berry was one of his graduate students. The computer had no central processing unit, but it did perform logical and other mathematical operations. Eckert and Mauchly, at the University of Pennsylvania, were interested in building a computer during the second world war. They were funded by the Department of Defense to build a machine to calculate trajectory tables for launching shells from ships. The computer, called ENIAC for Electronic Numerical Integrator and Computer, was unveiled in 1946, just after the war had ended. ENIAC was difficult to program since the program was written by plugging cables into a switch, similar to an old telephone switchboard.

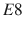 group was too complicated to map in Lies time. In fact, it wasnt until 2007 that the structure of the
group was too complicated to map in Lies time. In fact, it wasnt until 2007 that the structure of the 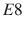 group could be mapped because the solution produced sixty times more data than the human genome project [1].
group could be mapped because the solution produced sixty times more data than the human genome project [1].









