Answers to Selected Exercises
Exercise )
| a. | (+ (* 1.2 (- 2 1/3)) -8.7) |
| b. | (/ (+ 2/3 4/9) (- 5/11 4/3)) |
| c. | (+ 1 (/ 1 (+ 2 (/ 1 (+ 1 1/2))))) |
| d. | (* (* (* (* (* (* 1 -2) 3) -4) 5) -6) 7) or (* 1 -2 3 -4 5 -6 7) |
Exercise )
See Section .
Exercise )
| a. | (car . cdr) |
| b. | (this (is silly)) |
| c. | (is this silly?) |
| d. | (+ 2 3) |
| e. | (+ 2 3) |
| f. | + |
| g. | (2 3) |
| h. | # |
| i. | cons |
| j. | 'cons |
| k. | quote |
| l. | 5 |
| m. | 5 |
| n. | 5 |
| o. | 5 |
Exercise )
(car (cdr (car '((a b) (c d)))))  b
b
(car (car (cdr '((a b) (c d)))))  c
c
(car (cdr (car (cdr '((a b) (c d))))))  d
d
Exercise )
'((a . b) ((c) d) ())
Exercise )
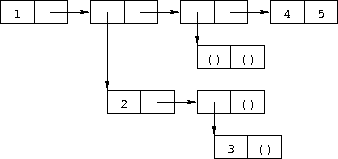
Exercise )
(car '((a b) (c d)))  (a b)
(a b)
(car (car '((a b) (c d))))  a
a
(cdr (car '((a b) (c d))))  (b)
(b)
(car (cdr (car '((a b) (c d)))))  b
b
(cdr (cdr (car '((a b) (c d)))))  ()
()
(cdr '((a b) (c d)))  ((c d))
((c d))
(car (cdr '((a b) (c d))))  (c d)
(c d)
(car (car (cdr '((a b) (c d)))))  c
c
(cdr (car (cdr '((a b) (c d)))))  (d)
(d)
(car (cdr (car (cdr '((a b) (c d))))))  d
d
(cdr (cdr (car (cdr '((a b) (c d))))))  ()
()
(cdr (cdr '((a b) (c d))))  ()
()
Exercise )
See Section .
Exercise )
- Evaluate the variables list, +, -, *, and /, yielding the list, addition, subtraction, multiplication, and division procedures.
- Apply the list procedure to the addition, subtraction, multiplication, and division procedures, yielding a list containing these procedures in order.
- Evaluate the variable cdr, yielding the cdr procedure.
- Evaluate the variable car, yielding the car procedure.
- Apply the car procedure to the list produced in step
- Evaluate the constants 17 and 5, yielding 17 and 5.
- Apply the subtraction procedure to 17 and 5, yielding 12.
Other orders are possible. For example, the variable car could have been evaluated before its argument.
Exercise )
| a. | (let ([x (* 3 a)]) (+ (- x b) (+ x b))) |
| b. | (let ([x (list a b c)]) (cons (car x) (cdr x))) |
Exercise )
The value is 54. The outer let binds x to 9, while the inner let binds x to 3 (9/3). The inner let evaluates to 6 (3 + 3), and the outer let evaluates to 54 (9 6).
Exercise )
| a. | (let ([x0 'a] [y0 'b])
(list (let ([x1 'c]) (cons x1 y0))
(let ([y1 'd]) (cons x0 y1)))) |
| b. | (let ([x0 '((a b) c)])
(cons (let ([x1 (cdr x0)])
(car x1))
(let ([x2 (car x0)])
(cons (let ([x3 (cdr x2)])
(car x3))
(cons (let ([x4 (car x2)])
x4)
(cdr x2)))))) |
Exercise )
Exercise )
See page .
Exercise )
| a. | no free variables |
| b. | + |
| c. | f |
| d. | cons, f, and y |
| e. | cons and y |
| f. | cons, y, and z (y also appears as a bound variable) |
Exercise )
The program would loop indefinitely.
Exercise )
(define compose
(lambda (p1 p2)
(lambda (x)
(p1 (p2 x)))))
(define cadr (compose car cdr))
(define cddr (compose cdr cdr))
Exercise )
(define caar (compose car car))
(define cadr (compose car cdr))
(define cdar (compose cdr car))
(define cddr (compose cdr cdr))
(define caaar (compose car caar))
(define caadr (compose car cadr))
(define cadar (compose car cdar))
(define caddr (compose car cddr))
(define cdaar (compose cdr caar))
(define cdadr (compose cdr cadr))
(define cddar (compose cdr cdar))
(define cdddr (compose cdr cddr))
(define caaaar (compose caar caar))
(define caaadr (compose caar cadr))
(define caadar (compose caar cdar))
(define caaddr (compose caar cddr))
(define cadaar (compose cadr caar))
(define cadadr (compose cadr cadr))
(define caddar (compose cadr cdar))
(define cadddr (compose cadr cddr))
(define cdaaar (compose cdar caar))
(define cdaadr (compose cdar cadr))
(define cdadar (compose cdar cdar))
(define cdaddr (compose cdar cddr))
(define cddaar (compose cddr caar))
(define cddadr (compose cddr cadr))
(define cdddar (compose cddr cdar))
(define cddddr (compose cddr cddr))
Exercise )
(define atom?
(lambda (x)
(not (pair? x))))
Exercise )
(define shorter
(lambda (ls1 ls2)
(if (< (length ls2) (length ls1))
ls2
ls1)))
Exercise )
The structure of the output would be the mirror image of the structure of the input. For example, (a . b) would become (b . a) and ((a . b) . (c . d)) would become ((d . c) . (b . a)).
Exercise )
(define append
(lambda (ls1 ls2)
(if (null? ls1)
ls2
(cons (car ls1) (append (cdr ls1) ls2)))))
Exercise )
(define make-list
(lambda (n x)
(if (= n 0)
'()
(cons x (make-list (- n 1) x)))))
Exercise )
See the description of list-ref on page .
Exercise )
(define shorter?
(lambda (ls1 ls2)
(and (not (null? ls2))
(or (null? ls1)
(shorter? (cdr ls1) (cdr ls2))))))
(define shorter
(lambda (ls1 ls2)
(if (shorter? ls2 ls1)
ls2
ls1)))
Exercise )
(define even?
(lambda (x)
(or (= x 0)
(odd? (- x 1)))))
(define odd?
(lambda (x)
(and (not (= x 0))
(even? (- x 1)))))
Exercise )
(define transpose
(lambda (ls)
(cons (map car ls) (map cdr ls))))












 b
b