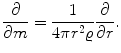1.1 Eulerian Description
For gaseous, non-rotating, single stars without strong magnetic fields, the only forces acting on a mass element come from pressure and gravity. This results in a spherically symmetric configuration. All functions will then be constant on concentric spheres, and we need only one spatial variable to describe them. It seems natural to use the distance r from the stellar centre as the spatial coordinate, which varies from r =0 at the centre to the total radius r = R at the surface of the star. In addition, the evolution in time t requires a dependence of all functions on t .If we thus take r and t as independent variables, we have a typical Eulerian treatment in the sense of classical hydrodynamics. Then all other variables are considered to depend on these two, for example, the density
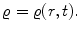
In order to provide a convenient description of the mass distribution inside the star, in particular of its effect on the gravitational field, we define the function). Then m varies with respect to r and t according to
The first term on the right is obviously the mass contained in the spherical shell of thickness dr (Fig.), and it gives the variation of m ( r , t ) due to a variation of r at constant t ,i.e.
Since it is preferable to describe the mass distribution in the star by m ( r , t ) (instead of
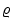
), () will be taken as the first of our basic equations in the Eulerian description.
Fig. 1.1
The variation of m with r at a fixed moment t = t 0. The quantities dm and dr are connected by ()
The last term in () gives the (spherically symmetric) mass flow out of the sphere of (constant) radius r due to a radial velocity v in the outward direction in the time interval dt:
The partial derivatives in the last two equations indicate as usual that the other independent variable ( t or r ) is held constant.
Differentiating () with respect to r and equating the two resulting expressions gives
This is the well-known continuity equation of hydrodynamics,
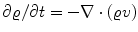
, for the special case of spherical symmetry.
1.2 Lagrangian Description
It will turn out that, in the spherically symmetric case, it is often more useful to take a Lagrangian coordinate instead of r , i.e. one which is connected to the mass elements. The spatial coordinate of a given mass element then does not vary in time. We choose for this coordinate the above defined m : to any mass element, the value m (which is the mass contained in a concentric sphere at a given momentt 0) is assigned once and for all (see Fig.).
The new independent variables are then m and t ,and all other variables are considered to depend on them, for example,
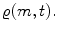
This also includes the radial distance r of our mass element from the centre, which is now described by the function r = r ( m , t ). Since there is certainly no singularity of
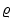
at the centre, we have here m =0, while the stars total mass m = M is reached at the surface (i.e. where r = R ).This already shows one advantage of the new description for the (normal) case of stars with constant total mass: while the radius R varies strongly in time, the star always extends over the same interval of the independent variable
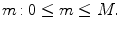
Although real stars do lose mass, for example, by stellar winds or due to gravitational interaction in binary systems, over short timescales the assumption of constant mass is justified nevertheless. In any case, the range of m never changes by more than a factor of a few.
As just indicated, there will certainly be no problem concerning a unique one-to-one transformation between the two coordinates r and m .We then easily find the connection between the partial derivatives in the two cases from well-known formulae. For any function depending on two variables, one of which is substituted by a new one (
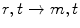
), the partial derivatives with respect to the new variables are given by
Subscripts indicate which of the spatial variables ( m or r ) is considered constant.
Let us apply the first of (). So we can solve for the last factor and obtain
This is a differential equation describing the spatial behaviour of the function r ( m , t ). It replaces () in the Lagrangian description and shall be the new first basic equation of our problem.
Introducing () gives the general recipe for the transformation between the two operators:
The second equation ()] would appear explicitly.
1.3 The Gravitational Field
It follows from elementary potential theory that, inside a spherically symmetric body, the absolute value g of the gravitational acceleration at a given distance r from the centre does not depend on the mass elements outside of r . It depends only on r and the mass within the concentric sphere of radius r , which we have called m :














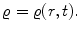
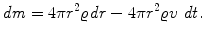
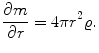
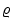 ), () will be taken as the first of our basic equations in the Eulerian description.
), () will be taken as the first of our basic equations in the Eulerian description. 
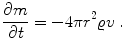
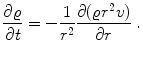
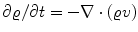 , for the special case of spherical symmetry.
, for the special case of spherical symmetry.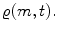 This also includes the radial distance r of our mass element from the centre, which is now described by the function r = r ( m , t ). Since there is certainly no singularity of
This also includes the radial distance r of our mass element from the centre, which is now described by the function r = r ( m , t ). Since there is certainly no singularity of 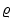 at the centre, we have here m =0, while the stars total mass m = M is reached at the surface (i.e. where r = R ).This already shows one advantage of the new description for the (normal) case of stars with constant total mass: while the radius R varies strongly in time, the star always extends over the same interval of the independent variable
at the centre, we have here m =0, while the stars total mass m = M is reached at the surface (i.e. where r = R ).This already shows one advantage of the new description for the (normal) case of stars with constant total mass: while the radius R varies strongly in time, the star always extends over the same interval of the independent variable 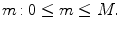 Although real stars do lose mass, for example, by stellar winds or due to gravitational interaction in binary systems, over short timescales the assumption of constant mass is justified nevertheless. In any case, the range of m never changes by more than a factor of a few.
Although real stars do lose mass, for example, by stellar winds or due to gravitational interaction in binary systems, over short timescales the assumption of constant mass is justified nevertheless. In any case, the range of m never changes by more than a factor of a few.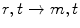 ), the partial derivatives with respect to the new variables are given by
), the partial derivatives with respect to the new variables are given by