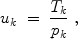Gianluigi Ferrari - Sensor Networks

Princeton University, Princeton, NJ, USA

H. Vincent Poor

Email:

Over the past 2025 years there has been considerable interest, and a number of major research developments, in the physical layer of wireless networks. Prominent examples include multiple-antenna (MIMO) systems [], to name just three. These major advances in the physical layer have made a major difference in the way we think about wireless networks at the link level. Although of course there remain many interesting and important open problems at the physical layer, since roughly the turn of this century interest in the area of wireless has shifted noticeably from the performance of individual links to the interactions among the nodes of the network. There are two basic modes of such interaction, competition and collaboration. Examples of competitive behavior in wireless networks include cognitive radio, in which users compete for spectrum; information theoretic security, in which an intended recipient of a message is in essence competing with an eavesdropper; and the use of game theory in the modeling, analysis and design of networks, in which sensors compete for the physical resources of a network to accomplish their own objectives. Alternatively, the use of collaboration among the nodes of a wireless network has also gained currency. Notable examples include network coding, cooperative transmission and relaying, multi-hop networking, collaborative beam-forming, and collaborative inference. All of these topics are areas that have arisen relatively recently in the community and they involve primarily node interactions rather than link layer issues.

These issues play no less a role in the design and analysis of wireless sensor networks than in other type of wireless network, and in this chapter, we will examine these two modes of node interaction by considering an illustrative example of each type that is particularly relevant to sensor networking. Both of these examples are addressing the key issue of energy efficiency, one by examining data transfer in a relatively basic setting, and the other by looking at the overarching application of the network. The first of these problem is the area of energy games in multiple access networks, in which sensors compete for wireless resources so as to optimize their individual energy efficiencies in transmitting data to a common access point, or data collection site. The other is the problem of collaborative inference, in which sensor terminals collaborate locally to perform distributed inference without the need to communicate their data to a common (possibly distant) access point. Each of these models has a role in practical sensor networks, and which is most relevant to a given system depends on the particular network deployment. Nevertheless, taken together, these examples illustrate some of the basic principles and issues arising in node-level behavior of wireless sensor networks.

We begin by considering the situation in which wireless sensors communicate their data to an access point via an infrastructure network using a multiple access protocol, as illustrated in Fig.. We can think of such a network as being like an economic system, in which the sensors behave as economic agents competing for resources in order to maximize their own utilities. (This view of network behavior is sometimes termed economorphic networking e.g., V. Rodriguez, 2008, personal communication.) In this case, utility is based on the transfer of data up to the access point as efficiently as possible. Because this is a multiple access network, the actions of one sensor affect the utilities of the other sensors. So, we can model this situation as a competitive, or non-cooperative, game, and we can examine the particular situation in which the utility to the sensors is measured in terms of energy efficiency that is, in bits-per-joule.

More specifically, we can think of a game having K players, where K is the number of sensors that are competing to communicate to the access point. Each sensor has a set of strategies, or actions ( A k for the k th sensor), and a utility function. Setting aside the set of strategies for now, as noted above the utility function of interest here is the energy efficiency, which can be measured as throughput divided by transmit power. That is, for sensor k , the utility can be written as

where T k denotes the sensors throughput (or, goodput, as we are interested only in successful transmissions) and p k denotes the sensors transmit power. Since throughput is measured in units of bits per second, and transmit power in units of watts, or joules per second, the units of this utility are bits-per-joule, as desired.

The transmit power p k in ( ], the frame success rate can be modeled as an instantaneous function, say f , of the received signal-to-interference-plus-noise ratio (SINR) with which that users transmissions are received at the access point, post processing but before data detection. This is, of course, an idealization, since we know that the frame success rate is not always an exact function of the SINR. But this is a reasonable approximation for many modulation formats and receivers of interest. The nice thing about this model is that it allows us to abstract the physical layer into the function f . That is, we can lump the entire physical layer, except for the SINR, into f . So, f includes all the things you might think as lying in the physical layer: the modulation, the noise and channel models, the packet length, and so forth. Because the SINR for a given user contains the transmitted power of that user in its numerator, and the powers of all the other users in its denominator (recall that this is a multiple-access channel), we can see why this is a competitive game: if one user turns up its transmit power, it will positively influence its own SINR and negatively influence the SINRs of all the other users. So, this is essentially a game on SINR.