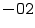An ever increasing amount of computational work is being relegated to computers, and often we almost blindly assume that the obtained results are correct. At the same time, we wish to accelerate individual computation steps and improve their accuracy. Numerical computations should therefore be approached with a good measure of skepticism. Above all, we should try to understand the meaning of the results and the precision of operations between numerical data.
A prudent choice of appropriate algorithms is essential (see, for example, []). In their implementation, we should be aware that the compiler may have its own will and has no clue about mathematical physics. In order to learn more about the essence of the computation and its natural limitations, we strive to simplify complex operations and restrict the tasks of functions to smaller, well-defined domains. It also makes sense to measure the execution time of programs (see Appendix J): large fluctuations in these well measurable quantities without modifications in running conditions typically point to a poorly designed program or a lack of understanding of the underlying problem.
1.1.1 Finite-Precision Arithmetic
The key models for computation with real numbers in finite precision are the floating-point and fixed-point arithmetic . A real number x in floating-point arithmetic with base is represented by the approximation
where
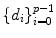
, d i {0,1,,1}, is a set of p integers and the exponent e is within [ e min, e max]. The expression m = d 0. d 1 d p 1 is called the significand or mantissa , while f =0. d 1 d p 1 is its fractional part . Here we are mostly interested in binary numbers (=2) which can be described by the fractional part f alone if we introduce two classes of numbers. The first class contains normal numbers with d 0=1; these numbers are represented as fl( x )=1. f 2 e , while the number zero is defined separately as
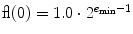
. The second class contains subnormal numbers, for which d 0=0. Subnormal numbers fall in the range between the number zero and the smallest positive normal number
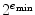
. They can be represented in the form
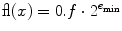
. Data types with single ( float ) and double ( double ) precision, as well as algorithms for computation of basic operations between them are defined by the IEEE 754 standard; see Table ].
Table 1.1
The smallest and largest exponents and approximate values of some important numbers representable in single- and double-precision floating-point arithmetic in base two, according to the IEEE 754 standard. Only positive values are listed
Precision | Single ( float ) | Double ( double ) |
|---|
e max | | 1023 |
e min=1 e max | | 1022 |
Smallest normal number | 1.181038 | 2.2310308 |
Largest normal number | 3.401038 | 1.8010308 |
Smallest representable number | 1.401045 | 4.9410324 |
Machine precision, M | 1.19107 | 2.221016 |
Format size | 32 bits | 64 bits |
Computations in fixed-point arithmetic (in which numbers are represented by a fixed value of e ) are faster than those in floating-point arithmetic, and become relevant when working with a restricted range of values. They becomes useful on very specific architectures where large speed and small memory consumption are crucial (for example, in GPS devices or CNC machining tools). In scientific and engineering work, floating-point arithmetic dominates.
The elementary binary operations between floating-point numbers are addition, subtraction, multiplication, and division. We denote these operations by
Since floating-point numbers have finite precision, the results of the operations x + y , x y , x y , and x / y , computed with exact values of x and y , are not identical to the results of the corresponding operations in finite-precision arithmetic, x y , x y , x y , and x y . One of the key properties of finite-precision arithmetic is the non-associativity of addition and multiplication,
This has important consequences, as demonstrated by the following examples.














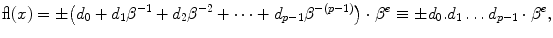
 , d i {0,1,,1}, is a set of p integers and the exponent e is within [ e min, e max]. The expression m = d 0. d 1 d p 1 is called the significand or mantissa , while f =0. d 1 d p 1 is its fractional part . Here we are mostly interested in binary numbers (=2) which can be described by the fractional part f alone if we introduce two classes of numbers. The first class contains normal numbers with d 0=1; these numbers are represented as fl( x )=1. f 2 e , while the number zero is defined separately as
, d i {0,1,,1}, is a set of p integers and the exponent e is within [ e min, e max]. The expression m = d 0. d 1 d p 1 is called the significand or mantissa , while f =0. d 1 d p 1 is its fractional part . Here we are mostly interested in binary numbers (=2) which can be described by the fractional part f alone if we introduce two classes of numbers. The first class contains normal numbers with d 0=1; these numbers are represented as fl( x )=1. f 2 e , while the number zero is defined separately as 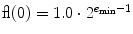 . The second class contains subnormal numbers, for which d 0=0. Subnormal numbers fall in the range between the number zero and the smallest positive normal number
. The second class contains subnormal numbers, for which d 0=0. Subnormal numbers fall in the range between the number zero and the smallest positive normal number 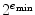 . They can be represented in the form
. They can be represented in the form 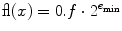 . Data types with single ( float ) and double ( double ) precision, as well as algorithms for computation of basic operations between them are defined by the IEEE 754 standard; see Table ].
. Data types with single ( float ) and double ( double ) precision, as well as algorithms for computation of basic operations between them are defined by the IEEE 754 standard; see Table ]. 

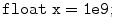
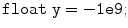
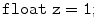 with the GNU compiler c ++ and option
with the GNU compiler c ++ and option