An Automata-Theoretic Approach to Modeling Systems and Specifications over Infinite Data
Abstract
Data-parameterized systems model finite state systems over an infinite data domain. VLTL is an extension of LTL that uses variables in order to specify properties of computations over infinite data, and as such VLTL is suitable for specifying properties of data-parameterized systems. We present Alternating Variable Bchi Word Automata (AVBWs), a new model of automata over infinite alphabets, capable of modeling a significant fragment of VLTL. While alternating and non-deterministic Bchi automata over finite alphabets have the same expressive power, we show that this is not the case for infinite data domains, as we prove that AVBWs are strictly stronger than the previously defined Non-deterministic Variable Bchi Word Automata (NVBWs). However, while the emptiness problem is easy for NVBWs, it is undecidable for AVBWs. We present an algorithm for translating AVBWs to NVBWs in cases where such a translation is possible. Additionally, we characterize the structure of AVBWs that can be translated to NVBWs with our algorithm, and identify fragments of VLTL for which a direct NVBW construction exists. Since the emptiness problem is crucial in the automata-theoretic approach to model checking, our results give rise to a model-checking algorithm for a rich fragment of VLTL and systems over infinite data domains.
Introduction
Infinite data domains become increasingly relevant and wide-spread in real-life systems, and are integral in communication systems, e-commerce systems, large databases and more. Systems over infinite data domains were studied in several contexts and especially in the context of datalog systems [], that are the standard of web documents.
Temporal logic, particularly LTL, is widely used for specifying properties of ongoing systems. However, LTL is unable to specify computations that handle infinite data. Consider, for example, a system of processes and a scheduler. If the set of processes is finite and known in advance, we can express and verify properties such as every process is eventually active. However, if the system is dynamic, in which new processes can log in and out, and the total number of processes is unbounded, LTL is unable to express such a property.
VLTL (LTL with variables) [] extends LTL with variables that range over an infinite domain, making it a natural logic for specifying ongoing systems over infinite data domains. For the example above, a VLTL formula can be
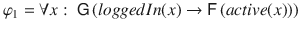
, where x ranges over the process IDs. Thus, the formula specifies that for every process ID, once it is logged in, it will eventually be active. Notice that this formula now specifies this property for an unbounded number of processes. As another example, the formula
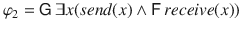
, where x ranges over the message contents (or message IDs), specifies that in every step of the computation, some message is sent, and this particular message is eventually received. Using variables enables handling infinitely many messages along a single computation.
In the automata-theoretic approach to model checking [], the authors suggested non-deterministic variable Bchi word automata (NVBWs), a model that augments NBWs with variables, and used it to construct a model-checking algorithm for a fragment of VLTL that is limited to
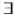
-quantifiers that appear only at the head of the formula.
The emptiness problem for NVBWs is NLOGSPACE-complete. Since the emptiness problem is crucial for model checking, NVBWs are an attractive model. However, they are quite weak. For example, NVBWs are unable to model the formula
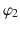
above.
In this work, we present a new model for VLTL specifications, namely alternating variable Bchi word automata (AVBWs). These are an extension of NVBWs, which we prove to be stronger and able to express a much richer fragment of VLTL. Specifically, we show that AVBWs are able to express the entire fragment of
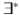
-VLTL, which is a fragment of VLTL with only
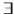
-quantifiers, whose position in the formula is unrestricted.
We now elaborate more on NVBWs and AVBWs. As mentioned, an NVBW
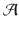
uses variables that range over an infinite alphabet
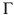
. A run of
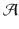
on a word w assigns values to the variables in a way that matches the letters in w . For example, if a letter a .8 occurs in w , then a run of
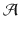
may read a . x , where x is assigned 8. In addition, the variables may be reset at designated states along the run, and so a . x can be later used for reading another letter a .5, provided that x has been reset. Resetting then allows reading an unbounded number of letters using a fixed set of variables. Another component of NVBWs is an inequality set
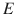
, that allows restricting variables from being assigned with the same value. Our new model of AVBWs extends NVBWs by adding alternation . An alternating automaton may split its run and continue reading the input along several different paths simultaneously, all of which must accept.
There is a well-known translation from LTL to ABW []. Thus, AVBWs are a natural candidate for modeling VLTL. Indeed, as we show, AVBWs are able to express all
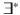
-VLTL, following a translation that is just as natural as the LTL to ABW translation. Existential quantifiers (anywhere) in the formula are translated to corresponding resets in the automaton. Moreover, unlike the finite alphabet case, in which NBWs and ABWs are equally expressive, in the infinite alphabet case alternation proves to be not only syntactically stronger but also semantically stronger, as we show that AVBWs are more expressive than NVBWs.
As we have noted, our goal is to provide a model which is suitable for a model-checking algorithm for VLTL, and that such a model should be easily tested for emptiness. However, we show that the strength of AVBWs comes with a price, and their emptiness problem is unfortunately undecidable. To keep the advantage of ease of translation of VLTL to AVBWs, as well as the ease of using NVBWs for model-checking purposes, we would then like to translate AVBWs to NVBWs, in cases where such a translation is possible. This allows us to enjoy the benefit of both models, and gives rise to a model-checking algorithm that is able to handle a richer fragment of VLTL than the one previously studied.













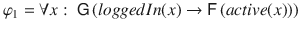 , where x ranges over the process IDs. Thus, the formula specifies that for every process ID, once it is logged in, it will eventually be active. Notice that this formula now specifies this property for an unbounded number of processes. As another example, the formula
, where x ranges over the process IDs. Thus, the formula specifies that for every process ID, once it is logged in, it will eventually be active. Notice that this formula now specifies this property for an unbounded number of processes. As another example, the formula 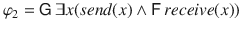 , where x ranges over the message contents (or message IDs), specifies that in every step of the computation, some message is sent, and this particular message is eventually received. Using variables enables handling infinitely many messages along a single computation.
, where x ranges over the message contents (or message IDs), specifies that in every step of the computation, some message is sent, and this particular message is eventually received. Using variables enables handling infinitely many messages along a single computation. -quantifiers that appear only at the head of the formula.
-quantifiers that appear only at the head of the formula.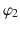 above.
above.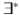 -VLTL, which is a fragment of VLTL with only
-VLTL, which is a fragment of VLTL with only 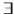 -quantifiers, whose position in the formula is unrestricted.
-quantifiers, whose position in the formula is unrestricted.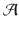 uses variables that range over an infinite alphabet
uses variables that range over an infinite alphabet 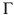 . A run of
. A run of 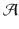 on a word w assigns values to the variables in a way that matches the letters in w . For example, if a letter a .8 occurs in w , then a run of
on a word w assigns values to the variables in a way that matches the letters in w . For example, if a letter a .8 occurs in w , then a run of 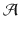 may read a . x , where x is assigned 8. In addition, the variables may be reset at designated states along the run, and so a . x can be later used for reading another letter a .5, provided that x has been reset. Resetting then allows reading an unbounded number of letters using a fixed set of variables. Another component of NVBWs is an inequality set
may read a . x , where x is assigned 8. In addition, the variables may be reset at designated states along the run, and so a . x can be later used for reading another letter a .5, provided that x has been reset. Resetting then allows reading an unbounded number of letters using a fixed set of variables. Another component of NVBWs is an inequality set 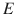 , that allows restricting variables from being assigned with the same value. Our new model of AVBWs extends NVBWs by adding alternation . An alternating automaton may split its run and continue reading the input along several different paths simultaneously, all of which must accept.
, that allows restricting variables from being assigned with the same value. Our new model of AVBWs extends NVBWs by adding alternation . An alternating automaton may split its run and continue reading the input along several different paths simultaneously, all of which must accept.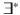 -VLTL, following a translation that is just as natural as the LTL to ABW translation. Existential quantifiers (anywhere) in the formula are translated to corresponding resets in the automaton. Moreover, unlike the finite alphabet case, in which NBWs and ABWs are equally expressive, in the infinite alphabet case alternation proves to be not only syntactically stronger but also semantically stronger, as we show that AVBWs are more expressive than NVBWs.
-VLTL, following a translation that is just as natural as the LTL to ABW translation. Existential quantifiers (anywhere) in the formula are translated to corresponding resets in the automaton. Moreover, unlike the finite alphabet case, in which NBWs and ABWs are equally expressive, in the infinite alphabet case alternation proves to be not only syntactically stronger but also semantically stronger, as we show that AVBWs are more expressive than NVBWs.