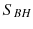1. Introduction
The goal of Loop Quantum Gravity (LQG) is to take two extremely well-developed and successful theories, General Relativity and Quantum Field Theory, at face value and attempt to combine them into a single theory with a minimum of assumptions and deviations from established physics. Our goal, as authors of this paper, is to provide a succinct but clear description of LQGthe main body of concepts in the current formulation of LQG relying primarily on the self-dual variables approach, some of the historical basis underlying these concepts, and a few simple yet interesting resultsaimed at the reader who has more curiosity than familiarity with the underlying concepts, and hence desires a broad, pedagogical overview before attempting to read more technical discussions. This paper is inspired by the view that one never truly understands a subject until one tries to explain it to others. Accordingly we have attempted to create a discussion which we would have wanted to read when first encountering LQG. Everyones learning style is different, and accordingly we make note of several other reviews of this subject [], which the reader may refer to in order to gain a broader understanding, and to sample the various points of view held by researchers in the field.
We will begin with a brief review of the history of the field of quantum gravity in the remainder of this section. Following this we review some topics in general relativity in Chap. along with a discussion of its present status and future prospects.
It is assumed that the reader has a minimal familiarity with the tools and concepts of differential geometry, quantum field theory and general relativity, though we aim to remind the reader of any relevant technical details as necessary.
Before we begin, it would be helpful to give the reader a historical perspective of the developments in theoretical physics which have led us to the present stage.
We are all familiar with classical geometry consisting of points, lines and surfaces. The framework of Euclidean geometry provided the mathematical foundation for Newtons work on inertia and the laws of motion. In the 19th century Gauss, Riemann and Lobachevsky, among others, developed notions of curved geometries in which one or more of Euclids postulates were loosened. The resulting structures allowed Einstein and Hilbert to formulate the theory of general relativity which describes the motion of matter through spacetime as a consequence of the curvature of the background geometry. This curvature in turn is induced by the matter content as encoded in Einsteins equations (). Just as the parallel postulate was the unstated assumption of Newtonian mechanics, whose rejection led to Riemmanian geometry, the unstated assumption underlying the framework of general relativity is that of the smoothness and continuity of spacetime on all scales.
Loop quantum gravity and related approaches invite us to consider the possibility that our notion of spacetime as a smooth continuum must give way to an atomistic description of geometry in which the classical spacetime we observe around us emerges from the interactions of countless (truly indivisible) atoms of spacetime. This idea is grounded in mathematically rigorous results, but is also a natural continuation of the trend that began when 19th century attempts to reconcile classical thermodynamics with the physics of radiation encountered fatal difficultiessuch as James Jeans ultraviolet catastrophe. These difficulties were resolved only when work by Planck, Einstein and others in the early 20th century provided an atomistic description of electromagnetic radiation in terms of particles or quanta of light known as photons . This development spawned quantum mechanics, and in turn quantum field theory, while around the same time the special and general theories of relativity were being developed.
In the latter part of the 20th century physicists attempted, without much success, to unify the two great frameworks of quantum mechanics and general relativity. For the most part it was assumed that gravity was a phenomenon whose ultimate description was to be found in the form of a quantum field theory as had been so dramatically and successfully accomplished for the electromagnetic, weak and strong forces in the framework known as the Standard Model. These three forces could be understood as arising due to interactions between elementary particles mediated by gauge bosons whose symmetries were encoded in the groups U (1), SU (2) and SU (3) for the electromagnetic, weak and strong forces, respectively. The universal presumption was that the final missing piece of this grand unified picture, gravity, would eventually be found in the form of the QFT of some suitable gauge group. This was the motivation for the various grand unified theories (GUTs) developed by Glashow, Pati-Salam, Weinberg and others where the hope was that it would be possible to embed the gravitational interaction along with the Standard Model in some larger group (such SO (5), SO (10) or
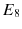
depending on the particular scheme). Such schemes could be said to be in conflict with Occams dictum of simplicity and Einstein and Diracs notions of beauty and elegance. More importantly all these models assumed implicitly that spacetime remains continuous at all scales . As we shall see this assumption lies at the heart of the difficulties encountered in unifying gravity with quantum mechanics.
A significant obstacle to the development of a theory of quantum gravity is the fact that GR is not renormalizable. The gravitational coupling constant G (or equivalently
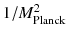
in dimensionless units where
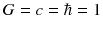
) is not dimensionless, unlike the fine-structure constant
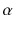
in QED. This means that successive terms in any perturbative series have increasing powers of momenta in the numerator. Rejecting the notion that systems could absorb or transmit energy in arbitrarily small amounts led to the photonic picture of electromagnetic radiation and the discovery of quantum mechanics. Likewise, rejecting the notion that spacetime is arbitrarily smooth at all scalesand replacing it with the idea that geometry at the Planck scale must have a discrete characterleads us to a possible resolution of the ultraviolet infinities encountered in quantum field theory and to a theory of quantum gravity.
Bekensteins observation [] of the relationship between the entropy of a black hole and the area of its horizon combined with Hawkings work on black hole thermodynamics led to the realization that there were profound connections between thermodynamics, information theory and black hole physics. These can be succinctly summarized by the famous area law relating the entropy of a macroscopic black hole
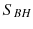












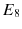 depending on the particular scheme). Such schemes could be said to be in conflict with Occams dictum of simplicity and Einstein and Diracs notions of beauty and elegance. More importantly all these models assumed implicitly that spacetime remains continuous at all scales . As we shall see this assumption lies at the heart of the difficulties encountered in unifying gravity with quantum mechanics.
depending on the particular scheme). Such schemes could be said to be in conflict with Occams dictum of simplicity and Einstein and Diracs notions of beauty and elegance. More importantly all these models assumed implicitly that spacetime remains continuous at all scales . As we shall see this assumption lies at the heart of the difficulties encountered in unifying gravity with quantum mechanics.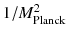 in dimensionless units where
in dimensionless units where 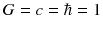 ) is not dimensionless, unlike the fine-structure constant
) is not dimensionless, unlike the fine-structure constant 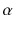 in QED. This means that successive terms in any perturbative series have increasing powers of momenta in the numerator. Rejecting the notion that systems could absorb or transmit energy in arbitrarily small amounts led to the photonic picture of electromagnetic radiation and the discovery of quantum mechanics. Likewise, rejecting the notion that spacetime is arbitrarily smooth at all scalesand replacing it with the idea that geometry at the Planck scale must have a discrete characterleads us to a possible resolution of the ultraviolet infinities encountered in quantum field theory and to a theory of quantum gravity.
in QED. This means that successive terms in any perturbative series have increasing powers of momenta in the numerator. Rejecting the notion that systems could absorb or transmit energy in arbitrarily small amounts led to the photonic picture of electromagnetic radiation and the discovery of quantum mechanics. Likewise, rejecting the notion that spacetime is arbitrarily smooth at all scalesand replacing it with the idea that geometry at the Planck scale must have a discrete characterleads us to a possible resolution of the ultraviolet infinities encountered in quantum field theory and to a theory of quantum gravity.