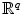We want to abstract the idea of distance because this notion often arises in mathematics. The concept must be general enough to encompass the circumstances under which it arises, but it should conform to the intuitive notion we all have of what is meant by the distance between two points. Because this is being done at the start of the first section, before proceeding it would be profitable for readers to reflect on what properties they think should be included in an abstract concept of distance; then they can compare these thoughts with the definition given below.
1.1 Definitions and Examples
Here is the accepted mathematical definition of an abstract distance.
Definition 1.1.1.
A metric space is a pair ( X , d ) where X is a set and d is a function d : X X [0,), called a metric , that satisfies the following properties for all x , y , z in X :
(a) d ( x , y )= d ( y , x );
(b) d ( x , y )=0 if and only if x = y ;
(c) (the triangle inequality) d ( x , y ) d ( x , z ) + d ( z , y ).
These three properties are usually part of what we intuitively would associate with the idea of distance. Condition (a) is sometimes called the reflexive property and says that the distance from x to y is the same as the distance from y to x . The second property says the obvious: the distance from a point to itself is 0 and the only point at a distance zero from x is x itself. The third, the triangle property, says that the shortest distance between two points is the direct onenot a distance involving a third point. One might be tempted to phrase this by saying that the shortest distance between two points is a straight line, but in this abstract setting we have no concept of a line, let alone a straight one.
It is certainly possible that some readers might have additional properties they would want a distance function to have, but the aforementioned properties are the minimal ones. Indeed, in mathematics there are several particular situations where additional axioms for a distance are assumed; those are more specialized theories, and what we are now going to explore is this basic one. Here are some examples of metric spaces.
Example 1.1.2.
(a)
Let
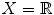
, the set of real numbers, and define d ( x , y )=| x y |. See Exercise 1.
(b)
Let
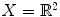
, the plane, and define
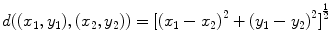
. Readers know from the Pythagorean Theorem that this is the straight-line distance, and they can use geometry to verify that this standard notion of the distance between two points satisfies the axioms in the preceding definition. More generally, we can define a metric on q -dimensional Euclidian space
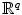
by
for x =( x 1,, x q ) and y =( y 1,, y q ) in
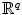
. However, proving that this satisfies the needed axioms, specifically the triangle inequality, requires some effort, and the proof will be given later (Corollary 1.1.5).
(c)
Let
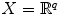
, q -dimensional Euclidean space, for x , y in
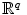
define
This is easier to verify as a metric (Exercise 2).
(d)
Again let
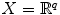
, and now define
Once again,
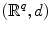
is a metric space (Exercise 3). It is worth observing that in each of the last three examples, when q =1, all these metrics are the standard absolute value on
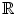
.
(e)
Let X be any set, and define
It is a simple exercise to verify that ( X , d ) is a metric space. This is called the discrete metric on X .
(f)
An important class of examples arises as follows. Suppose ( X , d )is given. If Y is a nonempty subset of X , then ( Y , d ) is a metric space and is referred to as a subspace . As a specific instance of this we can take
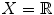
and Y =[0,1].
Now let us show that the function d given in part (b) of the preceding example is indeed a metric. To do this we need a famous inequality. Before presenting this inequality, we introduce the helpful notation that for vectors x =( x 1,, x q ) and y =( y 1,, y q ) in
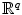
,
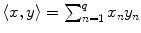
. Actually, this is more than just helpful notation as it denotes the inner or dot product in the vector space
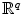
. This connection will not be explored here, however, and we will only regard this as notation. It is useful to observe the following properties for all vectors x , y , z in
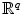














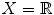 , the set of real numbers, and define d ( x , y )=| x y |. See Exercise 1.
, the set of real numbers, and define d ( x , y )=| x y |. See Exercise 1.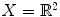 , the plane, and define
, the plane, and define 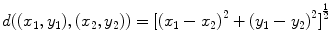 . Readers know from the Pythagorean Theorem that this is the straight-line distance, and they can use geometry to verify that this standard notion of the distance between two points satisfies the axioms in the preceding definition. More generally, we can define a metric on q -dimensional Euclidian space
. Readers know from the Pythagorean Theorem that this is the straight-line distance, and they can use geometry to verify that this standard notion of the distance between two points satisfies the axioms in the preceding definition. More generally, we can define a metric on q -dimensional Euclidian space 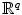 by
by 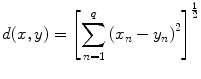
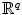 . However, proving that this satisfies the needed axioms, specifically the triangle inequality, requires some effort, and the proof will be given later (Corollary 1.1.5).
. However, proving that this satisfies the needed axioms, specifically the triangle inequality, requires some effort, and the proof will be given later (Corollary 1.1.5).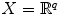 , q -dimensional Euclidean space, for x , y in
, q -dimensional Euclidean space, for x , y in 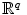 define
define 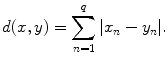
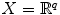 , and now define
, and now define 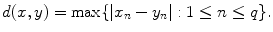
 is a metric space (Exercise 3). It is worth observing that in each of the last three examples, when q =1, all these metrics are the standard absolute value on
is a metric space (Exercise 3). It is worth observing that in each of the last three examples, when q =1, all these metrics are the standard absolute value on 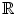 .
.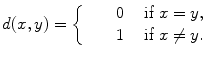
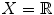 and Y =[0,1].
and Y =[0,1].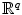 ,
, 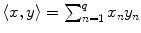 . Actually, this is more than just helpful notation as it denotes the inner or dot product in the vector space
. Actually, this is more than just helpful notation as it denotes the inner or dot product in the vector space 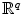 . This connection will not be explored here, however, and we will only regard this as notation. It is useful to observe the following properties for all vectors x , y , z in
. This connection will not be explored here, however, and we will only regard this as notation. It is useful to observe the following properties for all vectors x , y , z in