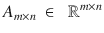Deep learning is a branch of machine learning that uses many layers of artificial neurons stacked one on top of the other for identifying complex features within the input data and solving complex real-world problems. It can be used for both supervised and unsupervised machine-learning tasks. Deep learning is currently used in areas such as computer vision, video analytics, pattern recognition, anomaly detection, text processing, sentiment analysis, and recommender system, among other things. Also, it has widespread use in robotics, self-driving car mechanisms, and in artificial intelligence systems in general.
Mathematics is at the heart of any machine-learning algorithm. A strong grasp of the core concepts of mathematics goes a long way in enabling one to select the right algorithms for a specific machine-learning problem, keeping in mind the end objectives. Also, it enables one to tune machine-learning/deep-learning models better and understand what might be the possible reasons for an algorithms not performing as desired. Deep learning being a branch of machine learning demands as much expertise in mathematics, if not more, than that required for other machine-learning tasks. Mathematics as a subject is vast, but there are a few specific topics that machine-learning or deep-learning professionals and/or enthusiasts should be aware of to extract the most out of this wonderful domain of machine learning, deep learning, and artificial intelligence. Illustrated in Figure are the different branches of mathematics along with their importance in the field of machine learning and deep learning. We will discuss the relevant concepts in each of the following branches in this chapter:
Figure 1-1
Importance of mathematics topics for machine learning and data science
Linear Algebra
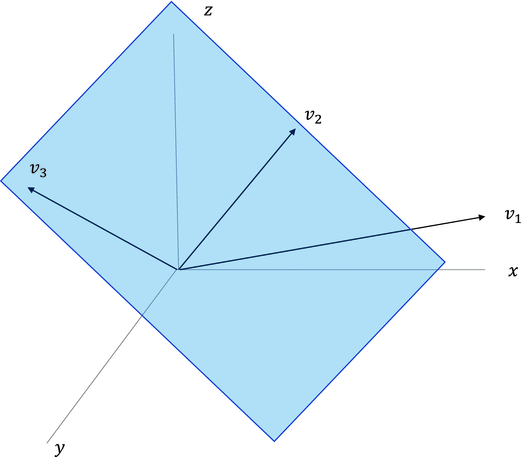
Linear algebra is a branch of mathematics that deals with vectors and their transformation from one vector space to another vector space. Since in machine learning and deep learning we deal with multidimensional data and their manipulation, linear algebra plays a crucial role in almost every machine-learning and deep-learning algorithm. Illustrated in Figure is a three-dimensional vector space where v 1, v 2 and v 3 are vectors and P is a 2-D plane within the three-dimensional vector space.
Figure 1-2
Three-dimensional vector space with vectors and a vector plane
Vector
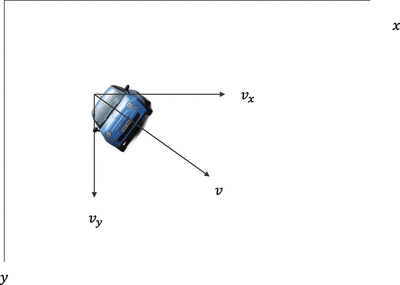
An array of numbers , either continuous or discrete, is called a vector, and the space consisting of vectors is called a vector space. Vector space dimensions can be finite or infinite, but most machine-learning or data-science problems deal with fixed-length vectors; for example, the velocity of a car moving in the plane with velocities Vx and Vy in the x and y direction respectively (see Figure ).
Figure 1-3
Car moving in the x-y vector plane with velocity components Vx and Vy
In machine learning, we deal with multidimensional data , so vectors become very crucial. Lets say we are trying to predict the housing prices in a region based on the area of the house, number of bedrooms, number of bathrooms, and population density of the locality. All these features form an input-feature vector for the housing price prediction problem.
Scalar
A one-dimensional vector is a scalar. As learned in high school, a scalar is a quantity that has only magnitude and no direction. This is because, since it has only one direction along which it can move, its direction is immaterial, and we are only concerned about the magnitude.
Examples: height of a child, weight of fruit, etc.
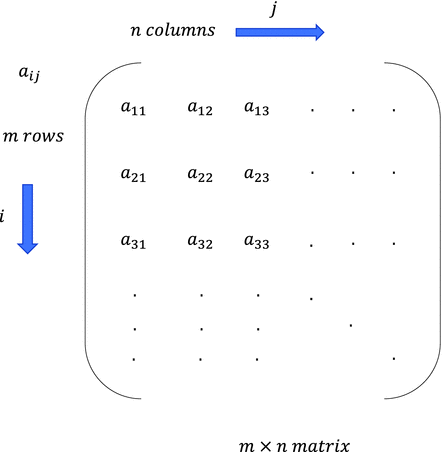
Matrix
A matrix is a two-dimensional array of numbers arranged in rows and columns. The size of the matrix is determined by its row length and column length. If a matrix A has m rows and n columns, it can be represented as a rectangular object (see Figure ) having
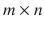
elements, and it can be denoted as
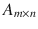
.
Figure 1-4a
Structure of a matrix
A few vectors belonging to the same vector space form a matrix.
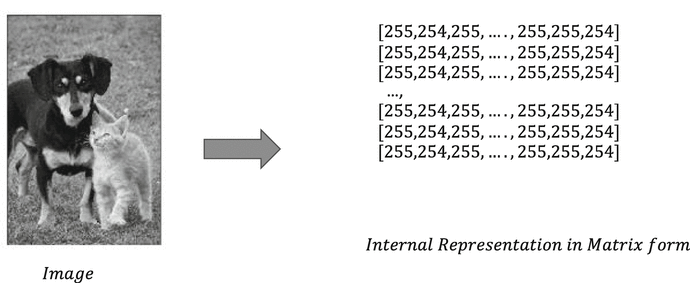
For example, an image in grayscale is stored in a matrix form. The size of the image determines the image matrix size, and each matrix cell holds a value from 0255 representing the pixel intensity. Illustrated in Figure is a grayscale image followed by its matrix representation.
Figure 1-4b
Structure of a matrix
Tensor
A tensor is a multidimensional array of numbers. In fact, vectors and matrices can be treated as 1-D and 2-D tensors. In deep learning, tensors are mostly used for storing and processing data. For example, an image in RGB is stored in a three-dimensional tensor, where along one dimension we have the horizontal axis and along the other dimension we have the vertical axis, and where the third dimension corresponds to the three color channels, namely Red, Green, and Blue. Another example is the four-dimensional tensors used in feeding images through mini-batches in a convolutional neural network. Along the first dimension we have the image number in the batch and along the second dimension we have the color channels, and the third and fourth dimensions correspond to pixel location in the horizontal and vertical directions .
Matrix Operations and Manipulations
Most deep-learning computational activities are done through basic matrix operations, such as multiplication, addition, subtraction, transposition, and so forth. Hence, it makes sense to review the basic matrix operations.
A matrix A of m rows and n columns can be considered a matrix that contains n number of column vectors of dimension m stacked side-by-side. We represent the matrix as









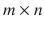 elements, and it can be denoted as
elements, and it can be denoted as 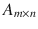 .
.