A SURVEY OF MATRIX THEORY AND MATRIX INEQUALITIES MARVIN MARCUS Professor of Computer Science University of California, Santa Barbara HENRYK MINC Professor of Mathematics University of California, Santa Barbara DOVER PUBLICATIONS, Inc., New YorkTo Arlen and Catherine Copyright 1964 by Marvin Marcus and Henryk Mine. Ail rights reserved under Pan American and International Copyright Conventions. This Dover edition, first published in 1992, is an unabridged, unaltered republication of the corrected (1969) printing of the work first published by Prindle, Weber & Schmidt, Boston, 1964, as Volume Fourteen of The Prindle, Weber & Schmidt Complementary Series in Mathematics. Library of Congress Cataloging-in-Publication Data Marcus, Marvin, 1927 A survey of matrix theory and matrix inequalities / Marvin Marcus, Henryk Mine, p. cm. Originally published: Boston : Prindle, Weber & Schmidt, 1969.
Includes bibliographical references. eISBN 13: 978-0-486-15306-3 1. Matrices. I. Mine, Henryk. Title. Title.
QA188.M36 1992 512.9434dc20 91-39704
CIP Manufactured in the United States by Courier Corporation
67102X05
www.doverpublications.com Preface M ODERN MATRIX THEORY is a subject that has lately gained considerable popularity both as a suitable topic for undergraduate students and as an interesting area for mathematical research. Apart from aesthetic reasons this is a result of the widespread use of matrices in both pure mathematics and the physical and social sciences. In this book we have tried within relatively few pages to provide a survey of a substantial part of the field. The first chapter starts with the assumption that the reader has never seen a matrix before, and then leads within a short space to many ideas which are of current research interest. In order to accomplish this within limited space, certain proofs that can be found in any of a very considerable list of books have been left out. However, we have included many of the proofs of classical theorems as well as a substantial number of proofs of results that are in the current research literature.
We have found that a subset of the material covered in Chapter I is ample for a one-year course at the third- or fourth-year undergraduate level. Of course, the instructor must provide some proofs but this is in accordance with our own personal preference not to regurgitate definition-theorem-proof from the printed page. There are many ideas covered in Chapter I that are not standard but reflect our own prejudices: e.g., Kronecker products, compound and induced matrices, quadratic relations, permanents, incidence matrices, (v, k, ) configurations, generalizations of commutativity, property L. The second chapter begins with a survey of elementary properties of convex sets and polyhedrons and goes through a proof of the Birkhoff theorem on doubly stochastic matrices. From this we go on to the properties of convex functions and a list of classical inequalities. This material is then put together to yield many of the interesting matrix inequalities of Weyl, Fan, Kantorovich, and others.
The treatment is along the lines developed by these authors and their successors and many of the proofs are included. This chapter contains an account of the classical Perron- Frobenius-Wielandt theory of indecomposable nonnegative matrices and ends with some very recent results on stochastic matrices. The third chapter is concerned with a variety of results on the localization of the characteristic roots of a matrix in terms of simple functions of its entries or of entries of a related matrix. The presentation is essentially in historical order, and out of the vast number of results in this field we have tried to cull those that seemed to be interesting or to have some hope of being useful. In general it is hoped that this book will prove valuable in some respect to anyone who has a question about matrices or matrix inequalities. M. M. H. M. M.
August, 1969 Special NotationCHAPTER IRreal numbers. Ccomplex numbers. Iintegers. Pnonnegative real numbers. F[]polynomial in with coefficients in F. Mn(F)n-square matrices with entries in F. A(i)ith row of A.A(j)jth column of A.Fkset of k-tuples of numbers from F. 0m,nmn zero matrix. Inn-square identity matrix. 0nn-tuple of zeros. ATtranspose of A.A*conjugate transpose of A.A conjugate of A.A B or
B or 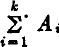 direct sum. ABKronecker product. Qk,ntotality of strictly increasing sequences of k integers chosen from 1, , n. Gk,ntotality of nondecreasing sequences of k integers chosen from 1, , n. Dk,ntotality of sequences of k distinct integers chosen from 1, , n. Sk,ntotality of sequences of k integers chosen from 1, , n. Ek(a)kth elementary symmetric function of the numbers a = (a1, , an). A[|], A[|), A(|], A(|)submatrices of A using rows numbered and columns numbered , rows and columns complementary to , etc. A[|], A[|), A(|], A(|)submatrices of A using rows numbered and columns numbered , rows and columns complementary to , etc.
direct sum. ABKronecker product. Qk,ntotality of strictly increasing sequences of k integers chosen from 1, , n. Gk,ntotality of nondecreasing sequences of k integers chosen from 1, , n. Dk,ntotality of sequences of k distinct integers chosen from 1, , n. Sk,ntotality of sequences of k integers chosen from 1, , n. Ek(a)kth elementary symmetric function of the numbers a = (a1, , an). A[|], A[|), A(|], A(|)submatrices of A using rows numbered and columns numbered , rows and columns complementary to , etc. A[|], A[|), A(|], A(|)submatrices of A using rows numbered and columns numbered , rows and columns complementary to , etc.
Here and are sequences of integers. Snsymmetric group of degree n. d(A)determinant of A.Cr(A)rth compound matrix of A.u1urskew-symmetric product of the vectors u1, , ur.Ek(A)sum of all k-square principal subdeterminants of A. tr (A)trace of A. p(A)permanent of A. Pr(A)rth induced matrix of A.u1ursymmetric product of the vectors u1, , ur.i(A)a characteristic root of A. x1, , xkspace spanned by x1, , xk. (A)nullity of A. I(i)(j) interchange rows i and j.II(i)+e(j)add c times row j to row i. IIIe(i) multiply row i by c.  I(i),(j)interchange columns i and j.II(i)+e(j)add c times column j to column i.IIIe(i)multiply column i by c.
I(i),(j)interchange columns i and j.II(i)+e(j)add c times column j to column i.IIIe(i)multiply column i by c.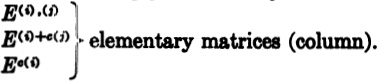 a | ba divides b.C(p())companion matrix of p(). H(p())hypercompanion matrix of p(). diag (a1, , an)the diagonal matrix with a1, , an down the main diagonal. CHAPTER IIU(in Chapter II) either of the sets Rn or Mm,n(R). x1, , xk)the orthogonal complement of the vector space spanned by x1 , xk.Dnset of all real n-square matrices with row and column sums equal to 1. nset of all n-square doubly stochastic matrices. H(X)convex hull of X.A * BHadamard product (the i,j entry is aijbij). CHAPTER III In Sections 1.2, 1.3, 1.4, and 1.6, the following special notation is used: for AMn(C
a | ba divides b.C(p())companion matrix of p(). H(p())hypercompanion matrix of p(). diag (a1, , an)the diagonal matrix with a1, , an down the main diagonal. CHAPTER IIU(in Chapter II) either of the sets Rn or Mm,n(R). x1, , xk)the orthogonal complement of the vector space spanned by x1 , xk.Dnset of all real n-square matrices with row and column sums equal to 1. nset of all n-square doubly stochastic matrices. H(X)convex hull of X.A * BHadamard product (the i,j entry is aijbij). CHAPTER III In Sections 1.2, 1.3, 1.4, and 1.6, the following special notation is used: for AMn(C
Next page












 B or
B or 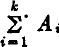 direct sum. ABKronecker product. Qk,ntotality of strictly increasing sequences of k integers chosen from 1, , n. Gk,ntotality of nondecreasing sequences of k integers chosen from 1, , n. Dk,ntotality of sequences of k distinct integers chosen from 1, , n. Sk,ntotality of sequences of k integers chosen from 1, , n. Ek(a)kth elementary symmetric function of the numbers a = (a1, , an). A[|], A[|), A(|], A(|)submatrices of A using rows numbered and columns numbered , rows and columns complementary to , etc. A[|], A[|), A(|], A(|)submatrices of A using rows numbered and columns numbered , rows and columns complementary to , etc.
direct sum. ABKronecker product. Qk,ntotality of strictly increasing sequences of k integers chosen from 1, , n. Gk,ntotality of nondecreasing sequences of k integers chosen from 1, , n. Dk,ntotality of sequences of k distinct integers chosen from 1, , n. Sk,ntotality of sequences of k integers chosen from 1, , n. Ek(a)kth elementary symmetric function of the numbers a = (a1, , an). A[|], A[|), A(|], A(|)submatrices of A using rows numbered and columns numbered , rows and columns complementary to , etc. A[|], A[|), A(|], A(|)submatrices of A using rows numbered and columns numbered , rows and columns complementary to , etc. I(i),(j)interchange columns i and j.II(i)+e(j)add c times column j to column i.IIIe(i)multiply column i by c.
I(i),(j)interchange columns i and j.II(i)+e(j)add c times column j to column i.IIIe(i)multiply column i by c.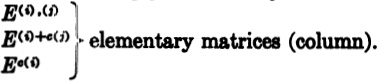 a | ba divides b.C(p())companion matrix of p(). H(p())hypercompanion matrix of p(). diag (a1, , an)the diagonal matrix with a1, , an down the main diagonal. CHAPTER IIU(in Chapter II) either of the sets Rn or Mm,n(R). x1, , xk)the orthogonal complement of the vector space spanned by x1 , xk.Dnset of all real n-square matrices with row and column sums equal to 1. nset of all n-square doubly stochastic matrices. H(X)convex hull of X.A * BHadamard product (the i,j entry is aijbij). CHAPTER III In Sections 1.2, 1.3, 1.4, and 1.6, the following special notation is used: for AMn(C
a | ba divides b.C(p())companion matrix of p(). H(p())hypercompanion matrix of p(). diag (a1, , an)the diagonal matrix with a1, , an down the main diagonal. CHAPTER IIU(in Chapter II) either of the sets Rn or Mm,n(R). x1, , xk)the orthogonal complement of the vector space spanned by x1 , xk.Dnset of all real n-square matrices with row and column sums equal to 1. nset of all n-square doubly stochastic matrices. H(X)convex hull of X.A * BHadamard product (the i,j entry is aijbij). CHAPTER III In Sections 1.2, 1.3, 1.4, and 1.6, the following special notation is used: for AMn(C