Ricciotti - P-Laplace equation in the Heisenberg group: regularity of solutions

The Author(s) 2015

Diego Ricciotti 1

(1)

Abstract

In this introductory chapter we present and motivate the result of this work concerning regularity of solutions to the p -Laplace equation in the Heisenberg group and we give an overview of some previous directly related results.

Keywords

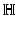The Heisenberg group is the simplest example of Carnot group, i.e. a connected, simply connected nilpotent Lie group 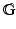whose associated Lie algebra 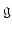admits a finite stratification. To be more precise we can identify, via the Exponential map, 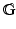with the Lie group 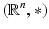where 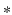is in general a non commutative group operation. The Lie algebra 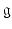admits a stratification in that it can be written as a direct sum of linear subspaces 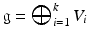such that 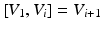where .

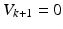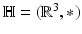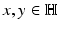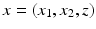For the first Heisenberg group indicating points by and 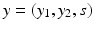the group operation is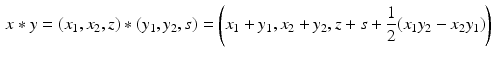 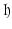and a basis of left-invariant vector fields for the associated Lie algebra is given by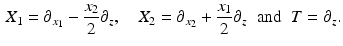 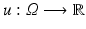If is a function from an open subset of 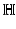we indicate by 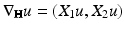the horizontal gradient of u .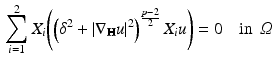

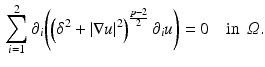
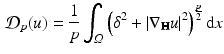
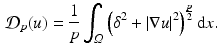
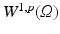This work deals with regularity o f weak solutions to the p -Laplace equation in the first Heisenberg group which is the subelliptic counterpart of the Euclidean p -Laplace equation Equations () are respectively the Euler-Lagrange equations for the p -Dirichlet functionals and It is customary to set this problem in the Sobolev space where it is easy to prove existence and uniqueness results and then try to recover the regularity of the solution. The same thing can be done in the Heisenberg group setting, where we have horizontal Sobolev spaces 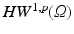of all 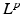functions whose horizontal derivatives are in 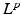. We say that 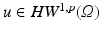is a weak solution of Eq. () if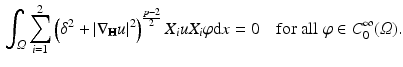 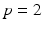The theory in the Euclidean case is well developed. The p -Laplace equation is a generalization of the classical Laplace equation which is the model for all elliptic linear equations. For the p -Laplacian coincides with the usual Laplace operator, but for 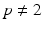the p -Laplace operator is non linear and degenerate if 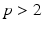or singular if 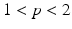where the gradient vanishes. The p -Laplace equation is not only relevant in Mathematical Analysis but also in the theory of quasi-conformal maps [] to quote only a few.

Concerning regularity matters, Uraltseva [] where they give an explicit formula relating k and