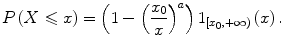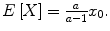Emanuela Rosazza Gianin and Carlo Sgarra UNITEXT Mathematical Finance: Theory Review and Exercises From Binomial Model to Risk Measures 10.1007/978-3-319-01357-2_1
Springer International Publishing Switzerland 2013
1. Short review of Probability and of Stochastic Processes
Abstract
Given a probability space (,
, P ), where denotes a non-empty set,
a -algebra and P a probability measure on :
A random variable (r.v.) is a function X : such that { : X () A } F for any Borel set A in .
A stochastic process is a family ( X t ) t 0 of random variables defined on (,
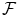
, P ).
The stochastic process ( X t ) t 0 is said to be a discrete-time stochastic process if t takes values in and a continuous-time stochastic process if t takes values in +.
A filtration on is a family
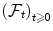
of -algebras on such that
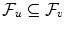
for any u v .
1.1 1.1 Review of Theory
Given a probability space (,
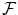
, P ), where denotes a non-empty set,
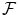
a -algebra and P a probability measure on :
A random variable (r.v.) is a function X : such that { : X () A } F for any Borel set A in .
A stochastic process is a family ( X t ) t 0 of random variables defined on (,
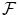
, P ).
The stochastic process ( X t ) t 0 is said to be a discrete-time stochastic process if t takes values in and a continuous-time stochastic process if t takes values in +.
A filtration on is a family
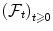
of -algebras on such that
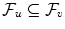
for any u v .
A stochastic process ( X t ) t 0 is called adapted to the filtration
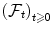
if, for any s 0, X s is
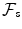
-measurable.
Given a stochastic process ( X t ) t 0, a filtration
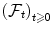
is said to be generated by ( X t )t=0 if, for any s 0,
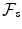
is the smallest -algebra that makes X s measurable.
A filtration can be interpreted as the evolution of the information available up to a given time.
For a more detailed and exhaustive treatment of the notions recalled here, we refer to the books of Mikosch [28] and Ross [34] .
The following families of random variables and stochastic processes are widely used in Mathematical Finance.
Bernoulli random variable
A random variable X has a Bernoulli distribution if it assumes only two values (typically 1 and 0) with probability p and (1 p ) respectively. In such a case, we write X B(p) .
As a consequence, the expected value and the variance of X are equal, respectively, to E[X] = p and V (X) = p(1 p) .
Binomial random variable and Binomial process
A binomial random variable Y n counts the number of successes in a series of n independent trials, where p is the probability of success in any one trial. In such a case, Y n Bin(n; p) .
Y n can be written as a sum Y n = i =1 n X i where ( X i ) i =1,..., n are independent and identically distributed (i.i.d.), X i B(p) and X i = 1 denotes a success in trial i . The expected value and the variance of a binomial random variable Y n Bin(n; p) are, respectively, E [ Y n [ = np and V ( Y n ) = np (1 p ).
The sequence
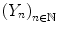
is called a binomial process.
Poisson random variable and Poisson process
A random variable Z has a Poisson distribution with parameter > 0 (in symbols, Z Poi ()) if it takes values in
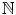
and its probability mass function is given by
for any n
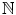
. Consequently, the expected value and the variance of Z are equal, respectively, to E [ Z ] = and to V ( Z ) = .
Furthermore, recall that a Poisson random variable can be obtained by taking the limit of a sequence of binomial random variables as p 0, n + and with pn = .
Setting = t (for t 0), can be understood as the rate or average number of arrivals per unit of time.
A process ( Z t ) t =0 is said to be a Poisson process of rate if Z 0 = 0 and if all the increments Z t Z s (for 0 s t ) are independent and identically distributed as a Poisson with parameter ( t s ).
If ( Z t ) t 0 is a Poisson process of rate counting the number of arrivals and T denotes the time between two arrivals, then T has an exponential distribution with parameter 0 ( T Exp ()). The density function of T is given by
The expected value and the variance of T are then equal to
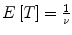
and
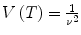
, respectively.
Pareto random variable
A random variable X has a Pareto distribution with parameters x 0 0 and a > 0 if its cumulative distribution function is given by
For a 1, X has finite expected value
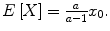












 , P ), where denotes a non-empty set,
, P ), where denotes a non-empty set,  a -algebra and P a probability measure on :
a -algebra and P a probability measure on : 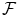 , P ).
, P ).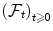 of -algebras on such that
of -algebras on such that 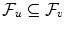 for any u v .
for any u v .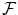 , P ), where denotes a non-empty set,
, P ), where denotes a non-empty set, 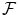 a -algebra and P a probability measure on :
a -algebra and P a probability measure on : 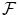 , P ).
, P ).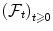 of -algebras on such that
of -algebras on such that 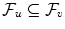 for any u v .
for any u v .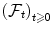 if, for any s 0, X s is
if, for any s 0, X s is 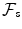 -measurable.
-measurable.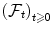 is said to be generated by ( X t )t=0 if, for any s 0,
is said to be generated by ( X t )t=0 if, for any s 0, 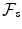 is the smallest -algebra that makes X s measurable.
is the smallest -algebra that makes X s measurable.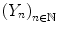 is called a binomial process.
is called a binomial process. and its probability mass function is given by
and its probability mass function is given by 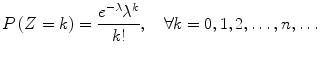
 . Consequently, the expected value and the variance of Z are equal, respectively, to E [ Z ] = and to V ( Z ) = .
. Consequently, the expected value and the variance of Z are equal, respectively, to E [ Z ] = and to V ( Z ) = .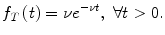
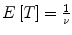 and
and 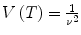 , respectively.
, respectively.