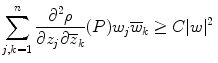In the early days of functional analysisthe early twentieth centurypeople did not yet know what a Banach space was nor a Hilbert space. They frequently studied a particular complete, infinite-dimensional space from a more abstract point of view. The most common space to be studied in this regard was of course L 2. It was when Stefan Bergman took a course from Erhard Schmidt on L 2 of the unit interval I that he conceived of the idea of the Bergman space of square-integrable holomorphic functions on the unit disc D . And the rest is history.
It is important for the Bergman theory that his space of holomorphic functions has an inner product structure and that it is complete. The first of these properties follows from the fact that it is a subspace of L 2; the second follows from a fundamental inequality that we shall consider in the next section.
1.1 The Bergman Kernel
It is difficult to create an explicit integral formula, with holomorphic reproducing kernel, for holomorphic functions on an arbitrary domain in
.]), will later be seen to have profound applications to the boundary regularity of holomorphic mappings.
Bungart [] have shown that any bounded domain in
will have a reproducing kernel for holomorphic functions such that the kernel itself is holomorphic in the free variable. In other words, the formula has the form
and K is holomorphic in the z variable. Of course Bungarts and Gleasons proofs are highly nonconstructive, and one can say almost nothing about the actual form of the kernel K . The venerable BochnerMartinelli kernel is easily constructed on any bounded domain with reasonable boundary (just as an application of Stokess theorem) and the kernel is explicit just like the Cauchy kernel in one complex variable. Also the kernel is the same for every domain. But the BochnerMartinelli kernel is definitely not holomorphic in the free variable. On the other hand, Henkin [, Chap. 10].
In fact this last described result was considered to be quite a dramatic advance. For Henkin, Kerzman, Ramirez, and GrauertLieb provided us with a fairly explicit kernel, with an explicit and measurable singularity, that can not only reproduce but also create holomorphic functions. Such a kernel is very much like the Cauchy kernel in one complex variable. Thus at least on strictly pseudoconvex domains, we can perform many of the activities to which we are accustomed from the function theory of one complex variable. We can get formulas for derivatives of holomorphic functions, we can analyze power series, we can consider an analogue of the Cauchy transform, and (perhaps most importantly) we can write down solution operators for the
problem. People were optimistic that these new integral formulas would give a shot in the arm to the theory of function algebrasthat they would now be able to study
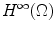
and
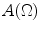
on a variety of domains in
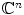
(see [, Chap. II, IV] for the role model in
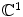
). But this turned out to be too difficult.
The Bergman kernel is a canonical kernel that can be defined on any bounded domain. It has wonderful invariance properties and is a powerful tool for geometry and analysis. But it is difficult to calculate explicitly.
In this section we will see some of the invariance properties of the Bergman kernel. This will lead in later sections to the definition of the Bergman metric (in which all biholomorphic mappings become isometries) and to such other canonical constructions as representative coordinates. The Bergman kernel has certain extremal properties that make it a powerful tool in the theory of partial differential equations (see Bergman and Schiffer []). Also the form of the singularity of the Bergman kernel (calculable for some interesting classes of domains) explains many phenomena of the function theory of several complex variables.
Let
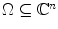
be a bounded domain (it is possible, but often tricky, to treat unbounded domains as well). Here a domain is a connected, open set. If the domain is smoothly bounded, then we may think of it as specified by a defining function :
It is customary to require that 0 on
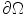
. One can demonstrate the existence of a definiting function by using the implicit function theorem. See [] for a detailed consideration of defining functions.
Given a domain
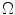
as described in the last paragraph and a point
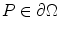
, we say that w is a complex tangent vector at P and write
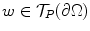
if
The point P is said to be strongly pseudoconvex if
for
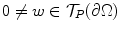
. In fact a little elementary analysis shows that we can write the defining property of strong pseudoconvexity as












 .]), will later be seen to have profound applications to the boundary regularity of holomorphic mappings.
.]), will later be seen to have profound applications to the boundary regularity of holomorphic mappings. will have a reproducing kernel for holomorphic functions such that the kernel itself is holomorphic in the free variable. In other words, the formula has the form
will have a reproducing kernel for holomorphic functions such that the kernel itself is holomorphic in the free variable. In other words, the formula has the form 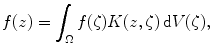
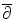 problem. People were optimistic that these new integral formulas would give a shot in the arm to the theory of function algebrasthat they would now be able to study
problem. People were optimistic that these new integral formulas would give a shot in the arm to the theory of function algebrasthat they would now be able to study 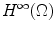 and
and  on a variety of domains in
on a variety of domains in 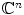 (see [, Chap. II, IV] for the role model in
(see [, Chap. II, IV] for the role model in 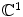 ). But this turned out to be too difficult.
). But this turned out to be too difficult.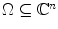 be a bounded domain (it is possible, but often tricky, to treat unbounded domains as well). Here a domain is a connected, open set. If the domain is smoothly bounded, then we may think of it as specified by a defining function :
be a bounded domain (it is possible, but often tricky, to treat unbounded domains as well). Here a domain is a connected, open set. If the domain is smoothly bounded, then we may think of it as specified by a defining function : 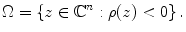
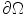 . One can demonstrate the existence of a definiting function by using the implicit function theorem. See [] for a detailed consideration of defining functions.
. One can demonstrate the existence of a definiting function by using the implicit function theorem. See [] for a detailed consideration of defining functions.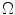 as described in the last paragraph and a point
as described in the last paragraph and a point 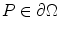 , we say that w is a complex tangent vector at P and write
, we say that w is a complex tangent vector at P and write 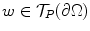 if
if 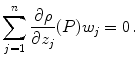
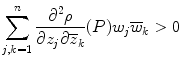
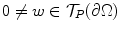 . In fact a little elementary analysis shows that we can write the defining property of strong pseudoconvexity as
. In fact a little elementary analysis shows that we can write the defining property of strong pseudoconvexity as