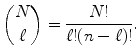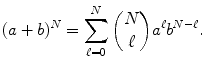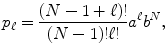1.1 Probability
Natural phenomena to which we assign a random character occur with great frequency. They are commonly characterized as unpredictable, irregular or erratic, and happen not only in the macroscopic world but also in the microscopic world. They are clearly distinguished from movements that we characterize as predictable, as with the fall of a compact solid body. An apple, for example, dropped a few meters from the ground, from the rest, will hit the ground at a point situated vertically below the point where it was released. If we observe the fall of a compact solid body, no matter how many times, we can see that the body will always fall at the same point. On the other hand, if we observe the fall of a body as light as a leaf, many times, we see that the leaf reaches different points of the ground, despite of being released from the same point, even in the complete absence of winds. The planar shape of the leaf associated with its small weight increase considerably the friction with the air, making the motion of the leaf irregular. The first trial, represented by the falling apple, is a predictable phenomenon, while the second, with the leaf, is an unpredictable erratic phenomenon, which we call random.
At first sight, one might think that a random phenomenon does not have a regularity and therefore would not be liable to a systematic study. However, after a careful observation, we see that it is possible, indeed, to find regularities in random phenomena. As an example, we examine the test in which a coin, biased or not, is thrown a number of times. The test is performed several times and for each test, that is, for each set of throws, we annotate the frequency of occurrences of heads, which is the ratio between the number of heads and the total number of throws. We can see that the frequencies obtained in different tests are very close to one another and the difference between them decreases as the number of throws in each test is increased.
Probability theory and its extensions, the theory of stochastic processes and stochastic dynamics, constitute the appropriate language for the description of random phenomena. They are based on two fundamental concepts: probability and random variable. The definition of probability is carried out by constructing the set of all outcomes of a given experiment, grouping them into mutually exclusive subsets. If, to each subset, one assigns a nonnegative real number such that their sum is equal to one, then we will be facing a probability distribution defined over the set of possible outcomes. We emphasize that this definition is very general and therefore insufficient for determining the probability to be associated with a particular experiment. The determination of the probability distribution that must be assigned to the results of a specific experiment is a major problem that must be solved by the construction of a theory or a model that describes the experiment.
The concept of probability, as well as any other physical quantity, has two basic aspects: one concerning its definition and the other concerning its interpretation. For most physical quantities, the two aspects are directly related. However, this does not happen with probability. The interpretation of probability does not follow directly from its definition. We interpret the probability of a certain outcome as the frequency of occurrence of the outcome, which constitutes the frequentist interpretation. In the example of the throw of a coin, we see that the probability of occurrence of heads is interpreted as being the ratio between the number of heads and the total number of throws. As happens to any experimental measurement, we should expect a difference between the frequency obtained experimentally and the probability assigned to the experiment. This difference however is expected to decrease as the number of throws increases and must vanish when this number grows without limits.














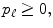
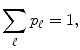

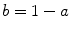 .
.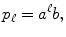
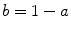 . The random variable takes the integer values 0,1,2, The normalization follows from the identity
. The random variable takes the integer values 0,1,2, The normalization follows from the identity 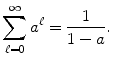
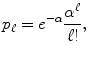
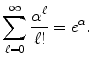
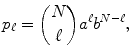
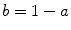 , and
, and