Robin Harte - Invertibility and Singularity for Bounded Linear Operators

INVERTIBILITY&SINGULARITYFOR BOUNDED LINEAR OPERATORSRobin HarteTrinity College, DublinDover Publications, Inc.Mineola, New YorkCopyright Copyright 1988, 2016 by Robin Harte All rights reserved. Bibliographical Note This Dover edition, first published in 2016, is an unabridged republication of the work originally published in 1988 by Marcel Dekker, Inc., New York and Basel, as part of the Pure and Applied Mathematics series. For this edition, the author has provided a new Prologue and Epilogue. Library of Congress Cataloging-in-Publication Data Names: Harte, Robin, 1938 Title: Invertibility and singularity for bounded linear operators / Robin Harte. Description: Dover edition. | Originally published: New York : Marcel Dekker, Inc., 1988. | Contains new prologue and epilogue. | Includes bibliographical references and index. | Includes bibliographical references and index.

Identifiers: LCCN 2016026995| ISBN 9780486810300 | ISBN 0486810305 Subjects: LCSH: Linear operators. | Singularities (Mathematics) Classification: LCC QA329.2 .H38 2016 | DDC 515/.7246dc23 LC record available at https://lccn.loc.gov/2016026995 Manufactured in the United States by RR Donnelley 81030501 2016 www.doverpublications.com for EMMA with love and squalor Prologue Gelfand Theory Unplugged In the beginning, there was Wiener: Norbert Wiener with his Tauberian theorem made the discovery that if a continuous periodic function effectively defined on the circle has an absolutely summable Fourier series, and never vanishes, then its reciprocal also has an absolutely summable Fourier series. Dually, an absolutely summable sequence of Fourier coefficients is convolution invertible if, and only if, a corresponding continuous function on the circle never vanishes. Similar results essentially hold for integrable functions on the real line and their Fourier transforms. The whole story can be repeated on locally compact abelian groups and their Pontrjagin duals. And then there was Gelfand: Israel Gelfand saw the Wiener algebra on a locally compact abelian group as the tip of an iceberg, replicated on a commutative Banach algebra.

A commutative Banach algebra comes with a maximal ideal space, and a generalization of the Fourier transform, sending Banach algebra elements to continuous functions on the maximal ideal space; now the Gelfand theory says that the Banach algebra element is invertible if, and only if, its Gelfand transform never vanishes. The electricity that powers the Gelfand theory is Zorns lemma and its maximal ideals, together with something called the Gelfand-Mazur lemma, which says that maximal ideals are always generated by multiplicative linear functionals. For an unplugged version, bypassing the elusive concept of maximal ideal, we introduce a joint spectrum, for finite tuples, and more general systems, of Banach algebra elements. The act of proof, extending the Gelfand-Mazur lemma, is a fundamental observation about the boundary of the spectrum, and the stage on which it is set is the old idea of a residual quotient, from commutative ideal theory. This book explores various kinds of non-singularity which are necessary conditions for invertibility, for single elements of linear algebras, more generally for finite and then arbitrary systems of elements. The spectrum of a complex linear algebra element aA is the set of those numbers C for which the scalar perturbation a fails to be invertible, building up a complex picture of the invertiblity pattern in A.

For more general n tuples a = (a1, a2, ..., an) An and systems a = (ax)xXAX the spectrum lies in Cn or CX. Subsets of the spectrum are generated by replacing invertibility by different kinds of non singularity. For systems p of non commutative polynomials we look for spectral mapping theorems p(a) = p(a). Spectral mapping theorems generally divide into forward theorems p(a) p(a) and backward theorems p(a) p(a); usually the forward theorems are easier and hold for general systems, while the backward theorems tend to be deeper, requiring the systems of elements aAX to be commutative and the algebra A to be complex Banach. In this book we have given detailed proofs of the fundamental background results such as the Hahn-Banach and Open Mapping theorems; some of the arguments can be partially developed in incomplete normed algebras. This for example helps to explain why the open mapping theorem works, while in an incomplete environment a compact operator in a sense carries around its own completeness.

The theory of the spectrum of a system of Banach algebra elements extends to the almost spectrum in an incomplete normed algebra; generally we try to lay out as much as possible of the Banach algebra proofs in the incomplete environment, and then make the conversion by folding in the completeness. We believe that this stratagem works particularly well for the open mapping theorem, but is distracting, and obscures the clear lines of what is happening, in the Fredholm and spectral theory. We have therefore written, as a sequel, a sort of bluffers guide by Vladimir Mller, who works through the vehicle of his regularity, which gives a unified account of many different kinds of non-singularity. Rather than attempt the massive amount of small corrections we would have liked to make to the reprinted material, and comprehensively update the bibliography, we refer the reader to . The epilogue serves in particular to introduce the old concept of residual quotient from commutative ideal theory, which serves as the stage on which the act of proof of the several variable spectral mapping theorem is performed. It also serves to present an inductive version of Taylor spectrum for commuting systems of Banach algebra elements, extending the discussion to general non commutative systems, in particular to quasi-commutative systems, and to commuting systems in Waelbroeck algebras.

The epilogue also comes with its own bibliography. References

R.E. Harte, Spectral mapping theorems, a bluffers guide, Springer 2014

V. Mller, Spectral theory of linear operators, Birkhauser Basel 2007

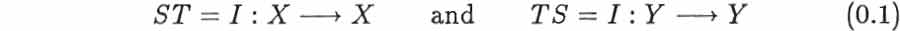Preface to the First Edition Suppose T : XY is a bounded linear operator between normed spaces: then T is said to be invertible if there is another bounded linear operator S : YX for which To be invertible an operator must obviously be nonsingular in various ways: for example, it must be one-one in the sense that 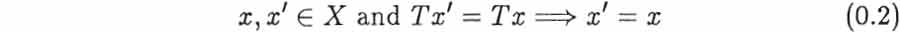and it must be onto in the sense that 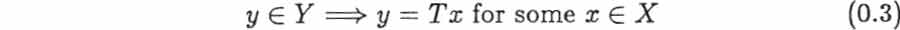It will be familiar that the conditions . This book is about the various kinds of nonsingularity that arise in this way, and their relationships with one another and with invertibility, together with relative analogs in which one operator is compared with another, essential analogs which hold to within finite dimensions, and algebraic analogs, aimed at ensuring that for example an inverse S should belong to some specified subspace of operators from Y to X. . .

In detail, as a sort of halfway stage, but find that we can do enough with them to achieve some of the simpler applications of Taylors theory, although of course not a functional calculus. We end the book with a pastiche of the functional calculus for commutative algebras, leaving the reader on the brink of Taylors construction. We have found and corrected hundreds of silly mistakes in this writing: we know that there remain as many uncorrected, and offer them as a series of unspoken exercises for the reader. More substantially, we have certainly not said the last word at several places in the book: for example we invite the reader to see if he can formulate a working concept of almost regular, fusing can be written out if completeness is built in from the start. It is impossible adequately to acknowledge all the help and advice we have had both during and before this writing: but Edward Bach of Trinity College looked hard at an early version of the first half of the book, and led us to a clearer picture of the relationship between enlargement and completeness, while Raul Curto in Iowa prevented us from making many silly mistakes toward the end. Others among those whose unpublished ideas appear in these pages are Ernst Albrecht, Manuel Gonzalez, Graeme Jameson, Martin Mathieu, Gerard Murphy, Miceal OSearcoid, Roger Smyth, Timothy Starr, Trevor West, Tony Wickstead, Tommy Wilansky, and Wieslaw Zelazko.

Next page