Minh Kha - Liouville-Riemann-Roch Theorems on Abelian Coverings

This series reports on new developments in all areas of mathematics and their applications - quickly, informally and at a high level. Mathematical texts analysing new developments in modelling and numerical simulation are welcome. The type of material considered for publication includes:

Texts which are out of print but still in demand may also be considered if they fall within these categories. The timeliness of a manuscript is sometimes more important than its form, which may be preliminary or tentative.

More information about this series at Titles from this series are indexed by Scopus, Web of Science, Mathematical Reviews, and zbMATH. http://www.springer.com/series/304

This Springer imprint is published by the registered company Springer Nature Switzerland AG.

The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland

Counting the number (i.e., dimension of the space) or even confirming the existence of solutions of an elliptic equation on a compact manifold (or in a bounded domain in 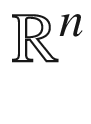) is usually a rather impossible task, unstable with respect to small variations of parameters. On the other hand, the Fredholm index of the corresponding operator, as it was conjectured by I. M. Gelfand [25] and proven by M. F. Atiyah and I. M. Singer [6, 7, 8, 9, 10], can be computed in topological terms. In particular, if the index of an operator L happens to be positive, this implies non-triviality of its kernel.

One might also be interested in index formulas in the case when the solutions are allowed to have some prescribed poles and have to have some mandatory zeros. Probably, the first result of this kind was the centuries old classical Riemann-Roch theorem [62, 63], which in an appropriate formulation provides the index of the 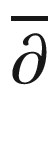-operator on a compact Riemannian surface, when a divisor of zeros and poles is provided. Analogs and extensions of this result were provided by V. G. Mazya and B. A. Plamenevskii [53] for elliptic boundary problems in domains and by N. S. Nadirashvili [57] for the Laplace-Beltrami operator on a complete compact. Riemannian manifold with a prescribed divisor. The latter result has been generalized by M. Gromov and M. A. Shubin [29, 30, 31] to computing indices of elliptic operators in vector bundles over compact (as well as non-compact) manifolds, when a divisor mandates a finite number of zeros and allows a finite number of poles of solutions.

On the other hand, Liouville type theorems count the number of solutions that allow to have a pole at infinity. Solution of an S.-T. Yaus problem [74, 75], given by T. H. Colding and W. P. Minicozzi II [16, 17, 18, 48], shows that on a Riemannian manifold of nonnegative Ricci curvature, the spaces of harmonic functions of fixed polynomial growths are finite dimensional. The result also applies to the Laplace-Beltrami operator on a nilpotent covering of a compact Riemannian manifold. No explicit formulas for these dimensions are available. However, an interesting case has been discovered by M. Avellaneda and F.-H. Lin [11] and J. Moser and M. Struwe [56]. It pertains periodic elliptic operators of divergent type, where exact dimensions can be computed and coincide with those for the Laplacian. This study has been extended by P. Li and J. Wang [49, 50] and brought to its natural limit in the case of periodic elliptic operators on co-compact abelian coverings by P. Kuchment and Y. Pinchover [43, 44].