Contents
Paraskevas Alvanos
Riemann-Roch Spaces and Computation Paraskevas Alvanos
Riemann-Roch Spaces and Computation
Managing Ediror: Aleksandra Nowacka-Leverton Associate Editor: Dimitris Poulakis Language Editor: Nick Rogers

Published by De Gruyter Open Ltd, Warsaw/Berlin Part of Walter de Gruyter GmbH, Berlin/Munich/Boston

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 license, which means that the text may be used for non-commercial purposes, provided credit is given to the author. For details go to http://creativecommons.org/licenses/by-nc-nd/3.0/. Copyright 2014 Paraskevas Alvanos published by De Gruyter Open ISBN 978-3-11-042613-7 e-ISBN 978-3-11-042612-0
Bibliographic information published by the Deutsche Nationalbibliothek The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available in the Internet at http://dnb.dnb.de. Managing Editor: Aleksandra Nowacka-Leverton Associate Editor: Dimitris Poulakis Language Editor: Nick Rogers www.degruyteropen.com Cover illustration: Paraskevas Alvanos
Contents

To my "
Flower" o
Tol o
Preface
Riemann-Roch space is a field of functions with applications in algebraic geometry and coding theory. This textbook is focused on theory and on computations that are relevant to Riemann-Roch spaces. It is noted that for the computation of integral points on curves, the study of a Riemann-Roch space is necessary (Alvanos et al., 2011; Poulakis et al., 2000; Poulakis et al., 2002).
Besides the computation of integral points on curves, computation of Riemann-Roch spaces are used for the construction of Goppa codes (Goppa, 1981; Goppa, 1988), symbolic parametrizations of curves (Van Hoeij, 1995; Van Hoeij, 1997), integration of algebraic functions (Davenport, 1981) and a lot more (Hiren et.al, 2005). Riemann-Roch space arises from the classical Riemann-Roch theorem which computes the dimension of the field of functions with specific zeros and poles dim D = deg Dg + 1 + i(D). Here D is a divisor, g is the genus of the function field and i(D) an invariant of the function field. The inequality dim D deg Dg + 1 was initially proved by Riemann (1857) and was upgraded to equality by Roch (1865). The scope of the textbook is not to add original research to the literature but to give an educational perspective on Riemann-Roch spaces and the computation of algebraic structures connected to Riemann-Roch theorem. The proofs of theorems that use stiff techniques are avoided, and proofs with educational value (according to the authors opinion) are presented, allowing the reader to follow the book without many difficult computation.
In order to follow the textbook, the reader should be aware of the basic algebraic structures such as group, ring, prime ideal, maximal ideal, number field, modules, vector spaces and the basics of linear algebra, matrix theory and polynomial theory. The first part of the textbook consists of four chapters where algebraic structures and some of their properties are analysed. The second part of the textbook consists of four more chapters where algorithms and examples connected to Riemann-Roch spaces are presented. Throughout the textbook a variety of examples cover the majority of the cases. This textbook is a rsum of the authors work and his research the last 15 years. Therefore, the author would like to thank all of his colleagues and friends that helped him in every way during those years.
Especially, the author would like to express his deep gratitude to his beloved wife, K. Roditou, for her comments and her support during the writing of this textbook. The author would also like to thank very much the referees for their corrections and their very thoughtful and useful comments and K. Chatzinikolaou for his suggestions about the design of the cover. Last but not least, the author would like to express his ultimate respect to his former supervisor and current mathematical mentor prof. Poulakis. 
Part I: Riemann-Roch Spaces
1 Elements of Algebra
In this first chapter we introduce the algebraic structures that will be used in the following chapters.

Part I: Riemann-Roch Spaces
1 Elements of Algebra
In this first chapter we introduce the algebraic structures that will be used in the following chapters.
Definitions are enriched with lots of examples and figures for better understanding. We will only deal with commutative rings and number fields and therefore every reference to a ring or a field implies a commutative ring and a number field respectively.
1.1 Domains
In this section we investigate some basic properties of domains that are used throughout the textbook. Starting with the algebraic structure of the commutative ring and adding properties to it, we establish the algebraic structure of the field.
Definition A commutative ring
R is called an
integral domain if for any two elements
a,
bR,
ab = 0 implies that
a = 0 or
b = 0. The definition of integral domain is necessary in order to have a domain where divisibility can occur.
As we know the set of nn invertible matrices, where the identity element of the ring is the identity matrix and the zero element of the ring is the zero matrix, form a commutative ring. The product of two matrices A, B might be the zero matrix while neither of A and B are zero matrices. For instance  Thus, the ring of nn diagonal matrices is not an integral domain, even though it is a commutative ring. All fields, the ring of rational integers
Thus, the ring of nn diagonal matrices is not an integral domain, even though it is a commutative ring. All fields, the ring of rational integers 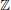 and all the subrings of integral domains are integral domains. Proposition 1.1.1.If R is an integral domain then R[x] is also an integral domain. Proof.
and all the subrings of integral domains are integral domains. Proposition 1.1.1.If R is an integral domain then R[x] is also an integral domain. Proof.
In order to prove that R[x] is an integral domain it is equivalent to prove that for any two elements 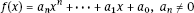 and
and 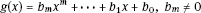 if f(x)g(x) = 0 then f(x) = 0 or g(x) = 0. The product f(x)g(x) is
if f(x)g(x) = 0 then f(x) = 0 or g(x) = 0. The product f(x)g(x) is 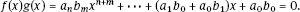 Thus
Thus













 Managing Ediror: Aleksandra Nowacka-Leverton Associate Editor: Dimitris Poulakis Language Editor: Nick Rogers
Managing Ediror: Aleksandra Nowacka-Leverton Associate Editor: Dimitris Poulakis Language Editor: Nick Rogers  Published by De Gruyter Open Ltd, Warsaw/Berlin Part of Walter de Gruyter GmbH, Berlin/Munich/Boston
Published by De Gruyter Open Ltd, Warsaw/Berlin Part of Walter de Gruyter GmbH, Berlin/Munich/Boston  This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 license, which means that the text may be used for non-commercial purposes, provided credit is given to the author. For details go to http://creativecommons.org/licenses/by-nc-nd/3.0/. Copyright 2014 Paraskevas Alvanos published by De Gruyter Open ISBN 978-3-11-042613-7 e-ISBN 978-3-11-042612-0 Bibliographic information published by the Deutsche Nationalbibliothek The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available in the Internet at http://dnb.dnb.de. Managing Editor: Aleksandra Nowacka-Leverton Associate Editor: Dimitris Poulakis Language Editor: Nick Rogers www.degruyteropen.com Cover illustration: Paraskevas Alvanos
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 license, which means that the text may be used for non-commercial purposes, provided credit is given to the author. For details go to http://creativecommons.org/licenses/by-nc-nd/3.0/. Copyright 2014 Paraskevas Alvanos published by De Gruyter Open ISBN 978-3-11-042613-7 e-ISBN 978-3-11-042612-0 Bibliographic information published by the Deutsche Nationalbibliothek The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available in the Internet at http://dnb.dnb.de. Managing Editor: Aleksandra Nowacka-Leverton Associate Editor: Dimitris Poulakis Language Editor: Nick Rogers www.degruyteropen.com Cover illustration: Paraskevas Alvanos  Thus, the ring of nn diagonal matrices is not an integral domain, even though it is a commutative ring. All fields, the ring of rational integers
Thus, the ring of nn diagonal matrices is not an integral domain, even though it is a commutative ring. All fields, the ring of rational integers 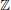 and all the subrings of integral domains are integral domains. Proposition 1.1.1.If R is an integral domain then R[x] is also an integral domain. Proof.
and all the subrings of integral domains are integral domains. Proposition 1.1.1.If R is an integral domain then R[x] is also an integral domain. Proof.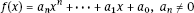 and
and 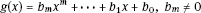 if f(x)g(x) = 0 then f(x) = 0 or g(x) = 0. The product f(x)g(x) is
if f(x)g(x) = 0 then f(x) = 0 or g(x) = 0. The product f(x)g(x) is 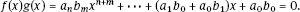 Thus
Thus