Ying Liu - Reliability Theory Based on Uncertain Lifetimes
Here you can read online Ying Liu - Reliability Theory Based on Uncertain Lifetimes full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2021, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Reliability Theory Based on Uncertain Lifetimes
- Author:
- Publisher:Springer
- Genre:
- Year:2021
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Reliability Theory Based on Uncertain Lifetimes: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Reliability Theory Based on Uncertain Lifetimes" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
This book, to reflect the systems diverse, relevant characteristics, uses three different mathematical tools, namely probability theory, fuzzy theory and random fuzzy theory, to model and analyze the reliability of each system. Reliability system engineering is an interdisciplinary area that chiefly focuses on the lifecycle characteristics of products and involves many fields of basic mathematics, technical science and management science. In recent years, there have been many books on reliability theory, but comparatively few on the reliability of mathematical models, or the reliability of mathematical models based on single probability theory or fuzzy theory. The findings presented here will not only enrich and expand traditional reliability theory, but also promote the development of related disciplines, lending the book considerable theoretical significance.
Ying Liu: author's other books
Who wrote Reliability Theory Based on Uncertain Lifetimes? Find out the surname, the name of the author of the book and a list of all author's works by series.













 be a nonempty set, and let
be a nonempty set, and let  be a -algebra over
be a -algebra over  . Each element in
. Each element in  is called an event. In order to present an axiomatic definition of probability, the following three axioms are assumed:
is called an event. In order to present an axiomatic definition of probability, the following three axioms are assumed: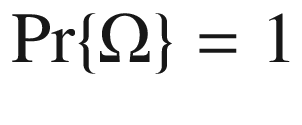 for the universal set
for the universal set  .
.