Volume 408
Studies in Fuzziness and Soft Computing
Series Editor
Janusz Kacprzyk
Systems Research Institute, Polish Academy of Sciences, Warsaw, Poland
The series Studies in Fuzziness and Soft Computing contains publications on various topics in the area of soft computing, which include fuzzy sets, rough sets, neural networks, evolutionary computation, probabilistic and evidential reasoning, multi-valued logic, and related fields. The publications within Studies in Fuzziness and Soft Computing are primarily monographs and edited volumes. They cover significant recent developments in the field, both of a foundational and applicable character. An important feature of the series is its short publication time and world-wide distribution. This permits a rapid and broad dissemination of research results.
Indexed by SCOPUS, DBLP, WTI Frankfurt eG, zbMATH, SCImago.
All books published in the series are submitted for consideration in Web of Science.
More information about this series at http://www.springer.com/series/2941
Jzsef Dombi and Orsolya Csiszr
Explainable Neural Networks Based on Fuzzy Logic and Multi-criteria Decision Tools
1st ed. 2021
Logo of the publisher
Jzsef Dombi
Institute of Informatics, University of Szeged, Szeged, Hungary
Orsolya Csiszr
Faculty of Basic Sciences, Esslingen University of Applied Sciences, Esslingen, Germany
Institute of Applied Mathematics, buda University, Budapest, Hungary
ISSN 1434-9922 e-ISSN 1860-0808
Studies in Fuzziness and Soft Computing
ISBN 978-3-030-72279-1 e-ISBN 978-3-030-72280-7
https://doi.org/10.1007/978-3-030-72280-7
The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG 2021
This work is subject to copyright. All rights are solely and exclusively licensed by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This Springer imprint is published by the registered company Springer Nature Switzerland AG
The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland
Foreword
In the traditional two-valued logic, each statement is either true or false. However, for imprecise (fuzzy) properties like small (or tall), in many cases, we are not 100% sure that some value is smallwe only have some degree of confidence that this value is small and some non-zero degree of confidence that this value is not small. This phenomenon is the main idea behind fuzzy logic. In fuzzy logic, for each property P and for each object x, for the statement P(x) (x has the property P), in addition to possible truefalse valueswhich in a computer are usually represented by 1 and 0we also have degrees of confidence that take intermediate values, i.e., values from the interval [0, 1].
In fuzzy logics, the law of contradiction (that 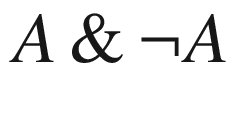 is always false) and the law of excluded middle (that
is always false) and the law of excluded middle (that  is always true) are, in general, false. However, these two laws are true for some fuzzy and and or operationsnamely for operations which are isomorphic to
is always true) are, in general, false. However, these two laws are true for some fuzzy and and or operationsnamely for operations which are isomorphic to 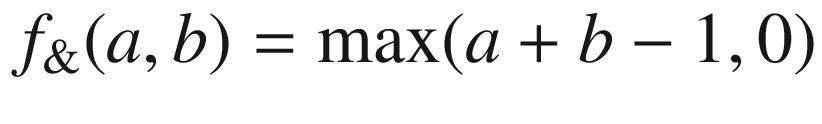 and
and 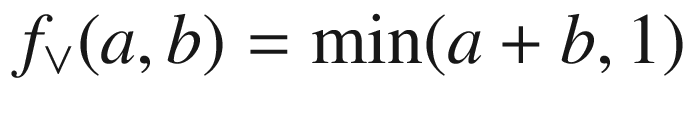 . These two types of operations are atypical, and, because of this, they are rarely studied and rarely used in applications.
. These two types of operations are atypical, and, because of this, they are rarely studied and rarely used in applications.
On the other hand, the law of contradiction and the law of excluded middle have an intuitive appeal. It is therefore reasonable to study fuzzy logics in which these two laws are satisfied. Such a study is one of the main foci of this book. It analyzes the triples of and, or, and not operations that satisfy these two laws and that arein some reasonable senseconsistent with each other. The book provides a full description of all such triplesand shows that for most such triples, we can define, in addition to the main negation, several additional negation operationswhich is also in good agreement with our intuition, where we usually distinguish between, e.g., the usual negation (such as not small) and a strong negation (such as large).
The authors also study how the need to be reasonably consistent with the corresponding triple affects implication operations, hedges (like very), and different averaging operationsranging from symmetric ones (that treat all the inputs equally) to weighted ones, where some inputs are given more weight than others. A very interesting (and innovative) part of the book is the study of preference operations  that describe to what extend b is preferable to a. These operations have many properties common with implication, as a result of which they are often identified with implication operations, but, as the authors show, there is a subtle but important difference.
that describe to what extend b is preferable to a. These operations have many properties common with implication, as a result of which they are often identified with implication operations, but, as the authors show, there is a subtle but important difference.
These parts are very interesting and important by themselves, but the most interesting part, in my opinion, is the relation with deep neural networks. In deep neural networks, data processing consists of interchangingly performing linear transformations and the rectified linear transformation 











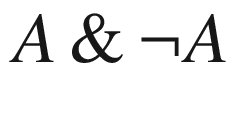 is always false) and the law of excluded middle (that
is always false) and the law of excluded middle (that  is always true) are, in general, false. However, these two laws are true for some fuzzy and and or operationsnamely for operations which are isomorphic to
is always true) are, in general, false. However, these two laws are true for some fuzzy and and or operationsnamely for operations which are isomorphic to 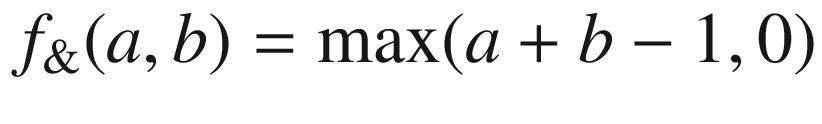 and
and 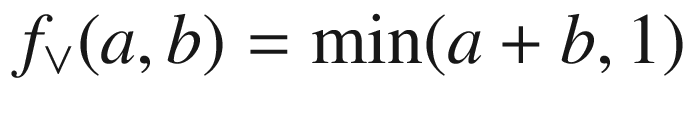 . These two types of operations are atypical, and, because of this, they are rarely studied and rarely used in applications.
. These two types of operations are atypical, and, because of this, they are rarely studied and rarely used in applications. that describe to what extend b is preferable to a. These operations have many properties common with implication, as a result of which they are often identified with implication operations, but, as the authors show, there is a subtle but important difference.
that describe to what extend b is preferable to a. These operations have many properties common with implication, as a result of which they are often identified with implication operations, but, as the authors show, there is a subtle but important difference.