Claude Brezinski - Extrapolation and Rational Approximation: The Works of the Main Contributors

Linear and nonlinear extrapolation methods are used for accelerating the convergence of sequences and series. Iterative procedures are widely employed in applied sciences. If the convergence of a sequence (of numbers, vectors, matrices, tensors,) is slow, or even when divergence occurs, these procedures have only a restricted practical interest. In some cases, it is possible to modify the iterative scheme to produce a sequence with better convergence properties. In other cases, one has no access to the algorithm building the sequence, which comes from a black box. The idea is then to transform the sequence into another one converging faster, under certain assumptions, to the same limit by a sequence transformation. When they are linear, sequence transformations are known and have been studied for a long time under the name of summation processes. They are attractive, since under quite mild conditions (Toeplitzs theorem), they transform any convergent sequence into a sequence converging to the same limit. However, their main drawback is the fact that each of them is only able to accelerate the convergence of quite particular classes of sequences.

This is one of the reasons why several nonlinear sequence transformations have been and are still defined and studied. It is necessary to speak in the plural, because it was proved that a sequence transformation able to accelerate the convergence of all sequences cannot exist. The same negative result is also true for some large classes of sequences such as, for example, monotonically decreasing sequences [.

Approximations of the limit, or antilimit, of a formal power series can be obtained by methods different from, but related, to the transformation of the sequence of its partial sums. Rational approximations of functions defined by their formal series expansion can be obtained by Pad approximants and Pad-type approximants, which are rational functions whose power series expansions in ascending powers of the variable agree with that of the given power series as far as possible. Series can also be transformed into continued fractions of various types by different methods. The successive convergents of a continued fraction are also rational functions, and some of them can coincide with Pad approximants. These two topics are strongly related to the theory of formal orthogonal polynomials (FOPs), a generalization of the usual ones. Other types of series such as Fourier series and series in Chebyshev polynomials can also be approximated by rational functions generalizing Pad approximants. Best rational approximation of functions is not considered in this book.

Continued fractions have a very long history, almost as long as the history of mathematics itself. For example, they are implied in Euclids method for the greatest common divisor and in the proofs of the transcendental character of the numbers and e. They were also instrumental in the development of orthogonal polynomials and in the spectral theory of operators. Pad approximants are more recent, but they go back several centuries []. They are much used in number theory and in the computation of the special functions encountered in mathematical physics.

The convergence and acceleration properties of sequence transformations have to be theoretically studied, and the degree of approximation and the convergence of these rational approximations also. Since they need to be implemented on a computer, it is necessary to design effective (usually recursive) algorithms for that purpose, and to code them in a programming language. Their numerical stability has to be studied, and the propagation of rounding errors as well. Finally, useful applications have to be found.

As can be seen in the figure below, sequence transformations, Pad approximants, and continued fractions have many interconnections with other important matters in applied mathematics and numerical analysis, some of which are developed herein.

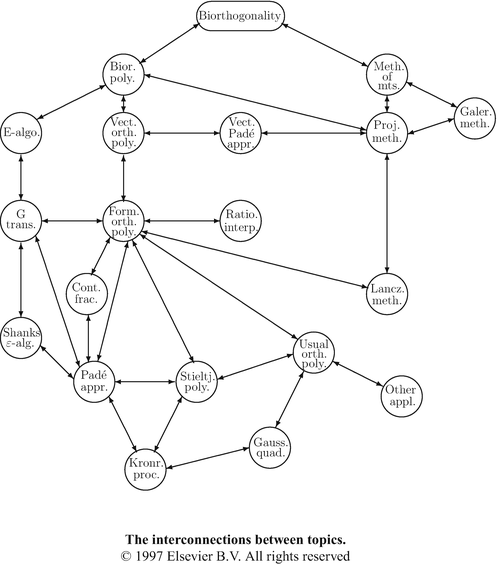
This book paints a fresco of the field of extrapolation and rational approximation over the last several centuries to the present through the works of their contributors. Simultaneously, it can serve as an introduction to the topics covered, which are extrapolation methods, Pad approximation, orthogonal polynomials, continued fractions, Lanczos-type methods, etc., and it describes the many links between them. In order that the reader may fully appreciate the works of the contributors, the book contains a quite precise description of the mathematical landscape on these subjects from the nineteenth century to the first part of the twentieth. Then, after an analysis of the works produced after that period (in particular those of Richardson, Aitken, Shanks, Wynn, and others), we give a review of the most recent developments of the domains concerned. Research is carried out by both women and men. This is why we also provide testimonies by several researchers who worked (and are still working) on these themes. They show the human side of research, and they furnish complementary views, and additional explanations and results. For the same reason, we sometimes indicate some personal facts about the people encountered. Biographies of various actors mentioned during our journey end the book.