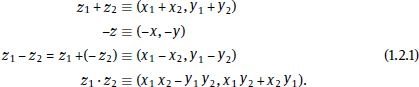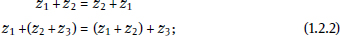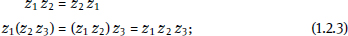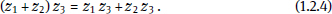Leslie Copley - Mathematics for the Physical Sciences

Leslie Copley

Mathematics for the Physical Sciences

Leslie Copley

Managing Editor: Paulina Lena-Szreter

Published by De Gruyter Open Ltd, Warsaw/Berlin
Part of Walter de Gruyter GmbH, Berlin/Munich/Boston

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 license, which means that the text may be used for non-commercial purposes, provided credit is given to the author. For details go to http://creativecommons.org/licenses/by-nc-nd/3.0/.

Copyright 2014 Leslie Copley
ISBN: 978-3-11-040945-1
e-ISBN: 978-3-11-040947-5

Bibliographic information published by the Deutsche Nationalbibliothek
The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available in the Internet at http://dnb.dnb.de.
Managing Editor: Paulina Lena-Szreter
www.degruyteropen.com
Cover illustration: Istock/VikaSuh

This book is based on lecture notes written and rewritten for mathematical methods courses given at both the undergraduate and graduate levels over a period of more than 30 years. The suggestion that I write a book was first made by students in one of those courses back in 1982. It seemed like a good idea but like many good ideas had to await a window of opportunity. The window did not open until I had completed a number of other projects and more especially until I had completed a 14 year stint in academic administration. Work began in earnest only in 1999 and even then only on a part-time basis, competing for attention with the demands of yet another administrative assignment. Retirement in 2005 finally removed professional distractions and slow but steady progress ensued.

It was always my intention to make the book freely accessible through posting on the internet. The book is in pdf format and can be downloaded chapter by chapter.

Curricular change is often driven by resource considerations and can result in considerable variability in the sequencing of topics. Necessity has proven to me that presenting boundary value problems before introducing complex analysis or even Fourier analysis is quite feasible. Nevertheless, I believe that the sequence adopted in this book beginning with complex analysis and proceeding through Fourier analysis and the solution of ordinary differential equations to boundary value problems is optimal.

While I solve a large number of example problems in the course of presenting theory, I have not included lists of suggested problems at the end of chapters. This omission is due to two observations. The first is that students seldom attempt problems other than those they are assigned and the second is that instructors already have many excellent sources to use when constructing their assignments.

Readers will discover that the proofs of theorems are sometimes included and sometimes not. As I told my students inclusion occurs only if the proof is educational. By this I meant only if the proof provides some insight into how to apply the theory. Thus, the (rigorous) proof of Cauchys theorem is excluded but the proofs of its many corollaries are included.

No matter how exhaustively a book is edited some errors or infelicities will always persist. Readers who detect any are invited to bring them to my attention at . I invite as well any comments you may have whether favourable or otherwise and more especially any suggestions on how to improve the text.

Physics is concerned with phenomena that are describable in terms of measurable quantities that assume real values. This is the basis of our intuitive understanding of the nature and significance of real numbers. It suggests as well that physicists deal primarily with functions of a real variable. Nevertheless, the theory of functions of a complex variable is one of the most important cornerstones of mathematical physics.

The uses of complex analysis range from the pedestrian one of providing notational simplification in the formulation of certain problems, (cyclotron dynamics for example), to that of furnishing the most elegant and evocative way of expressing the basic assumptions in certain physical theories. An example of the latter is the use of dispersion relations in optics and in the quantum theory of scattering; another treats momentum, energy and even angular momentum as complex variables to acquire an enhanced understanding of the outcome of collisions between subatomic particles. In between the pedestrian and the exotic are such applications as the evaluation of real definite integrals, the solution of potential problems in two dimensions, and the determination of the asymptotic behaviour of functions. Underlying them all is the fact that complex analysis permits a complete determination of functions on the basis of very limited detailed knowledge. Thus, it offers a much more powerful language for the discussion of the properties of the functions of interest to physicists than does real variable analysis.

What follows is a review of some foundational concepts of complex analysis. We start with the definition of complex number and of the rules of complex arithmetic and these may not look as familiar as the word review implies. That is because we shall use formal definitions that emphasize the distinction that exists between the complex and real number systems.

Definition: A complex number z is an ordered pair of real numbers, x and y say,

z (x, y);

x is called the real part and y the imaginary part of z:

x Re z, y Im z.

Definition: Two complex numbers z1 (x1, y1) and z2 (x2, y2) are equal if and only if their real and imaginary parts are separately equal; that is,

z1 = z2 if and only if x1 = x2 and y1 = y2.

Definition: If z1 (x1, y1) and z2 (x2, y2), then

Armed with these definitions of the fundamental operations, one can readily show that the standard laws of real number arithmetic apply to complex numbers as well:

(i) the commutative and associative laws of addition,

(ii) the commutative and associative laws of multiplication,

(iii) the distributive law,