Steffen Staab - Handbook on Ontologies

Handbook on Ontologies — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Handbook on Ontologies" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...256

Ontology Representation Languages

Springer-Verlag Berlin Heidelberg 2009

Steffen Staab and Rudi Studer (eds.) Handbook on Ontologies International Handbooks on Information Systems 10.1007/978-3-540-92673-3_0

What Is an Ontology?

Nicola Guarino 1

(1)

ITSC-CNR, Laboratory for Applied Ontology, 38100 Trento, Italy

(2)

SAP Research, CEC Karlsruhe, 76131 Karlsruhe, Germany

(3)

University of Koblenz-Landau, ISWeb, 56016 Koblenz, Germany

Nicola Guarino (Corresponding author)

Email:

Daniel Oberle

Email:

Steffen Staab

Email:

Summary

The word ontology is used with different senses in different communities. The most radical difference is perhaps between the philosophical sense, which has of course a well-established tradition, and the computational sense, which emerged in the recent years in the knowledge engineering community, starting from an early informal definition of (computational) ontologies as explicit specifications of conceptualizations. In this paper we shall revisit the previous attempts to clarify and formalize such original definition, providing a detailed account of the notions of conceptualization and explicit specification , while discussing at the same time the importance of shared explicit specifications.

Introduction

The word ontology is used with different meanings in different communities. Following [ as the science of being qua being, i.e., the study of attributes that belong to things because of their very nature. Unlike the experimental sciences, which aim at discovering and modeling reality under a certain perspective, Ontology focuses on the nature and structure of things per se, independently of any further considerations, and even independently of their actual existence. For example, it makes perfect sense to study the Ontology of unicorns and other fictitious entities: although they do not have actual existence, their nature and structure can be described in terms of general categories and relations.

In the second case, which reflects the most prevalent use in Computer Science, we refer to an ontology as a special kind of information object or computational artifact. According to [], the account of existence in this case is a pragmatic one: For AI systems, what exists is that which can be represented.

Computational ontologies are a means to formally model the structure of a system, i.e., the relevant entities and relations that emerge from its observation, and which are useful to our purposes. An example of such a system can be a company with all its employees and their interrelationships. The ontology engineer analyzes relevant entities The backbone of an ontology consists of a generalization/specialization hierarchy of concepts, i.e., a taxonomy. Supposing we are interested in aspects related to human resources, then Person , Manager , and Researcher might be relevant concepts, where the first is a superconcept of the latter two. Cooperates-with can be considered a relevant relation holding between persons. A concrete person working in a company would then be an instance of its corresponding concept.

In 1993, Gruber originally defined the notion of an ontology as an explicit specification of a conceptualization [] merged these two definitions stating that: An ontology is a formal, explicit specification of a shared conceptualization.

All these definitions were assuming an informal notion of conceptualization, which was discussed in detail in []. In the following, we shall revisit such discussion, by focusing on the three major aspects of the definition by Studer et al.:

• What is a conceptualization ?
• What is a proper formal, explicit specification ?
• Why is shared of importance?

It is the task of this chapter to provide a concise view of these aspects in the following sections. It lies in the nature of such a chapter that we have tried to make it more precise and formal than many other useful definitions of ontologies that do exist but that do not clarify terms to the degree of accuracy that we target here.

Accordingly, the reader new to the subject of ontologies may prefer to learn first about applications and examples of ontologies in the latter parts of this book and may decide to return to this opening chapter once he wants to see the common raison dtre behind the different approaches.

What is a Conceptualization ?

Gruber [], who claim: A body of formally represented knowledge is based on a conceptualization: the objects, concepts, and other entities that are assumed to exist in some area of interest and the relationships that hold among them. A conceptualization is an abstract, simplified view of the world that we wish to represent for some purpose. Every knowledge base, knowledge-based system, or knowledge-level agent is committed to some conceptualization, explicitly or implicitly.

Despite the complex mental nature of the notion of conceptualization, Genesereth and Nilsson choose to explain it by using a very simple mathematical representation: an extensional relational structure.

Definition 2.1 (Extensional relational structure)

An extensional relational structure , (or a conceptualization according to Genesereth and Nilsson ), is a tuple (D, R ) where

• D is a set called the universe of discourse
• R is a set of relations on D

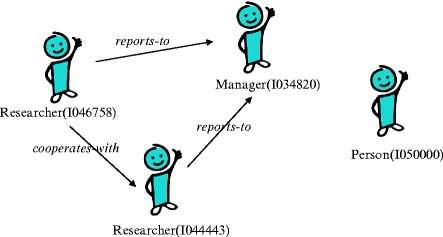
Note that, in the above definition, the members of the set R are ordinary mathematical relations on D , i.e., sets of ordered tuples of elements of D . So each element of R is an extensional relation, reflecting a specific world state involving the elements of D , such as the one depicted in Fig. , concerning the following example.

Fig. 1

A tiny part of a specific world with persons, managers, researchers, and their relationships in the running example of human resources in a large software company

Example 2.1

Let us consider human resources management in a large software company with 50,000 people, each one identified by a number (e.g., the social security number, or a similar code) preceded by the letter I. Let us assume that our universe of discourse D contains all these people, and that we are only interested in relations involving people. Our R will contain some unary relations, such as Person, Manager, and Researcher, as well as the binary relations reports-to and cooperates-with. The corresponding extensional relation structure (D , R ) looks as follows :

• D ={I000001,..., I050000,...}
• R = { Person , Manager, Researcher , cooperates with, reports to }

Relation extensions relations reflect a specific world. Here, we assume that Person comprises the whole universe D and that Manager and Researcher are strict subsets of D. The binary relations reports-to and cooperates-with are sets of tuples that specify every hierarchical relationship and every collaboration in our company. Some managers and researchers are depicted in Fig.. Here, I046758, a researcher, reports to his manager I034820, and cooperates with another researcher, namely I044443 .

• Person = D
• Manager = {... , I034820,... }
• Researcher = {... , I044443,... , I 046758,... }

Next page

1234567...256

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Handbook on Ontologies»

Look at similar books to Handbook on Ontologies. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Steffen Lehmann

Designing for Zero Waste

Steffen Mau

European Societies: Mapping Structure and Change

Steffen Ducheyne (editor)

Reassessing the Radical Enlightenment

Joo Hwa Philip Bay and Steffen Lehmann

Growing Compact: Urban Form, Density and Sustainability

Lamy Jean-Baptiste

Ontologies with Python: Programming OWL 2.0 Ontologies with Python and Owlready2

Travis Steffen

Viral Hero

Dix Steffen

Portuguese Modernisms: Multiple Perspectives in Literature and the Visual Arts

Steffen Mau

The Metric Society

Steffen

Ethics and Experience : Moral Theory from Just War to Abortion.

Steffen Saifer

Hot Skills; Developing Higher-Order Thinking In Young Learners

Robert Arp

Building Ontologies with Basic Formal Ontology

Jerome O. Steffen

Comparative frontiers, a proposal for studying the American West

Discussion, reviews of the book Handbook on Ontologies and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.