Sieve Methods
HEINI HALBERSTAM
and HANS-EGON RICHERT DOVER PUBLICATIONS, INC. Mineola, New York
Copyright Copyright 1974, 2011 by Heini Halberstam and the Estate of Hans-Egon Richert. All rights reserved.
Bibliographical Note This Dover edition, first published in 2011, is an unabridged republication of the work originally published in 1974 by Academic Press, Inc., London. Heini Halberstam has provided a new Preface and a new Errata List for this edition. (Heini) Sieve methods / Heini Halberstam and Hans-Egon Richert. p. cm. cm.
Originally published: London; New York: Academic Press, 1974. Includes bibliographical references and index. eISBN-13: 978-0-486-32080-9 1. Sieves (Mathematics) I. Richert, H.-E. Title. Title.
QA246.H35 2011 512.7.3dc22 2010039623 Manufactured in the United States by Courier Corporation 47939001 www.doverpublications.com
Preface to the Dover Edition
There is never a right time to publish a systematic account of a subject that is in a state of healthy growth; even as the late Ted Richert and I were embarking on the writing of
Sieve Methods forty years ago, inspired by the 1965 seminal of Jurkat and Richert, the young Henryk Iwaniec was discovering what has become known as the Rosser-Iwaniec method, which has since lead to many advances and applications, by himself and others. There is now in the literature an enveloping sieve (Hooley), a vector sieve (Brudern and Fourvy), a prime detecting sieve (Harman); and probably there will be others. There are now also other books about sieves that the interested reader might wish to consult: there is the influential discussion of sieves by one of the founders of the subject, Atle Selberg, in Volume II of his
Collected Papers (1991), there is
Sieves in Number Theory (2001) by the late George Greaves, there is Glyn Harmans monograph on Prime Detecting Sieves (2007), and recently Harold Diamond and I have published
A Higher Dimensional Sieve Method (2009), building on Iwaniecs approach. Several current books on Number Theory also devote sections or chapters to sieves. Our book has by now been long out of print, but demand for it continues and second-hand copies, when they can be found, command exorbitant prices. I am very grateful therefore to Dover Publications for reprinting it.
I apologize for the long list of Errata; that they were necessary in the original was entirely my fault. Heini Halberstam March, 2010
Preface
We conceived the idea of writing an introduction to applicable sieve theory during a brief encounter at Syracuse airport in the spring of 1966; we had both been lecturing on sieves, and it seemed to us that the time for a systematic exposition was long overdue. Our original plan was modest: to to supply, in lecture notes form, the theoretical background for the method of Jurkat-Richert [1] and to illustrate it by means of significant applications; also, to give a first connected account of the large sieve. As we burrowed in the literature and came to realize its extent and wealththe notes we prepared on some two hundred papers in the summer of 1968 alone would have filled a monographthe inadequacy of our original conception became increasingly clear. Not only did we find that we should have to assimilate much classical material into a revised scheme but, as we progressed, new results began to appear which affected it profoundly; so much so that, viewing the matter in retrospect, if we had called a halt at any earlier stage and published then, the book would have been much the poorer. In the end we abandoned the chapters on the large sieve altogetherhappily the monographs of Montgomery [2] and Huxley [2] have appeared in the meantime and provide admirable introductions to that subject and much else besideand concentrated on the small sieves of Brun and Selberg; even so, critics should have no trouble in pointing to omissions, and we accept any such criticisms in advance.
Indeed, we have been at pains to point out important extensions that time and space forced us to exclude, and we hope only that what we have done here will make it easier for others to cover these too in due course. The intermittent opportunities we have had of working together on the book have often shared the nature of that first encounter; even so, they would have been much rarer still but for the generous support of the National Science Foundation and of the U.S. Army Research Office, and for the equally generous hospitality of Syracuse University during several happy summers of uninterrupted work. We express our due gratitude to these institutions for all their help. We owe a special word of thanks also to Dr. C. C.
Vaughan of Imperial College, London, for having read with great care several chapters of the manuscript and for having removed some blemishes that had escaped our notice; also for having pointed out to us a . The final version of the manuscript was typed by Mrs. Shoshana Mandel of Tel Aviv University and Mrs. Angela Fullerton of Nottingham, and we are indebted to them both for undertaking a task that must often have been extremely trying. We thank the London Mathematical Society for accepting the book into their series of research monographs. Finally, we are grateful to Academic Press for all their help and patience during the course of publication; Mr.
Hitchings, of Roystan Printers Ltd., told us that our manuscript had been typographically the most difficult he had met in twenty years of printing mathematics. The companionship of a shared endeavour has been a memorable experience for us both. Now that we have completed, with a mixture of sadness and relief, the task we set ourselves eight years ago, we hope that there will be some readers for whom our book will prove to be a helpful introduction to a beautiful topic that has been shrouded for too long in unnecessary mystery. July, 1974 H. Halberstam H. -E.
Richert
Contents
Notation
STANDARD NOMENCLATURE
[
x] always denotes the largest integer not exceeding
x. Where no confusion is possible with the notation for intervals, (
a,
b) denotes the highest common factor of integers
a,
b and [
a,
b] their lowest common multiple. We denote the Mbius function by (
n) (for a definition see ). We write
v(
n) for the number of distinct prime divisors of
n, (
n) for the number of prime divisors of
n counted according to multiplicity, (
n) for the number of positive integer divisors of
n, and (
n) for Eulers function (the order of the multiplicative group of reduced residue classes modulo
n). We denote the number of primes not exceeding
x by (
x) and the number of primes not exceeding
x that are congruent to
l modulo
k by (
x;
k,
l).
SIEVE NOTATION
Throughout,
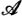
stands for the general integer sequence to be sifted and
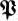
for a sifting set of primes.
The special sets 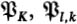 are defined on pages 24, 73 respectively. The following table indicates where the various principal functions featuring in our account of sieves are first introduced:
are defined on pages 24, 73 respectively. The following table indicates where the various principal functions featuring in our account of sieves are first introduced:
| the multiplicative functions | | on page |
| g |
| the remainders | rd |
| Rd |
| the summatory functions | G(z) |
| Gk(z) |
| G(x, z) |
| the products | |













 stands for the general integer sequence to be sifted and
stands for the general integer sequence to be sifted and 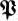 for a sifting set of primes.
for a sifting set of primes. 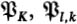 are defined on pages 24, 73 respectively. The following table indicates where the various principal functions featuring in our account of sieves are first introduced:
are defined on pages 24, 73 respectively. The following table indicates where the various principal functions featuring in our account of sieves are first introduced: