Jim Henle - The Proof and the Pudding: What Mathematicians, Cooks, and You Have in Common

THE PROOF AND THE PUDDING

Jim Henle

THE PROOF AND THE PUDDING

What Mathematicians, Cooks, and You Have in Common

Princeton University Press
Princeton and Oxford

Copyright 2015 by Princeton University Press

Published by Princeton University Press, 41 William Street, Princeton, New Jersey 08540

In the United Kingdom: Princeton University Press, 6 Oxford Street, Woodstock, Oxfordshire OX20 1TW

press.princeton.edu

Jacket illustration by Leon Steinmetz

Cartoons by Leon Steinmetz

All Rights Reserved

Library of Congress Cataloging-in-Publication Data

Henle, James M.

The proof and the pudding : what mathematicians, cooks, and you have in common / Jim Henle.

pages cm

Includes bibliographical references and index.

ISBN 978-0-691-16486-1 (hardback : alk. paper) 1. Mathematical recreations. 2. MathematicsMiscellanea. 3. CookingMiscellanea. 4. FoodMiscellanea. I. Title.

QA99.H46 2015

510dc23

2014049572

British Library Cataloging-in-Publication Data is available

This book has been composed in Baskerville 10 Pro

Printed on acid-free paper.

Printed in the United States of America

1 3 5 7 9 10 8 6 4 2

CONTENTS

PREFACE

THE PREMISE of this book is that if you look at mathematics and gastronomy the right way, they are amazingly alike. The goal of this book is to explore the two and to reveal their essential similarity.

But of course, math and cooking arent the same. You dont eat numbers. You cant take the square root of a muffin. And for most diners, a real bowl of spaghetti is more satisfying than any number of theoretical feasts. But thats the wrong attitude.

Instead, were going to think about what cooking and math do have in common: They began as crafts, simple and useful. They evolved into arts, complex and pleasurable. Both are presented, often, as lists of instructions. Both feature taste. Both pose difficulties. Both celebrate champions. Both intimidate novices.

Thats just the start.

But you must be warned. This book is about mathematics and cooking, but it wont draw any connection between them. In particular, there are no applications of math to cooking. Math is useful in the kitchen, sometimes, but thats not what this book is about.

Furthermore, mathematics itself isnt the point of this book. Ill show you some math, really cool math (incredible stuff, actually), but the purpose will be to illustrate features of mathematics. This isnt a math book.

Food, also, is not the point. There are recipes, good recipes, frighteningly good recipes (you have no idea). But they serve a higher purpose. This isnt a cookbook.

After reading The Proof and the Pudding, you may know more math. And you may know more about cooking. But that would be incidental. The goal is for you to see mathematics and gastronomy in a new way, as fraternal twins.

I intend to convince you that

1. We do math and we cook for more or less the same reasons.

2. We solve math problems with the same attitudes and tools we use to solve problems in the kitchen.

3. We judge mathematics with many of the same criteria we use to judge food.

4. And in general, life in mathematics and life in gastronomy are remarkably similar. Mathematicians and cooks have similar dreams, similar fears, and similar guilty secrets.

Theres more that I want to say about cooking and math. I have gastronomic and mathematical views on aesthetics, creativity, inspiration, strategy, genius, and depravity. I thought Id put them into one book.

And one more thing. This book has a deeper purpose. Underneath the propositions and the pastry, the real subject of this book is fun.

There are reasons to do mathematics and there are reasons to cook. But in both fields, the chief motivation is pleasure. This is not hard to see on the gastronomic side, but mathematicians also, surprisingly, are hedonists. Theyre out for a good time.

I dont want to sound immodest, but I think Im good at having fun. You can ask my friends. Theyll all tell you I have more fun than I should.

I can find pleasure in repetitive tasks. I can enjoy hopeless quests. I can have fun making serious mistakes.

If theres something Im interested in, I will pursue it to excess. I will spend happy hours covering sheets of papers with straight lines and covering sheets of dough with pats of butter.

Im not sure what this adds up to, but theres a zen to it and I have it. And Id like to share it.

ACKNOWLEDGMENTS

I AM indebted to so many.

There are those who helped me with proofs. There are those who helped me with puddings. There are those whose support for the project and the ideas were crucial to its realization. There are members of my family who walk these pages, seen and unseen. Finally, as the poet says, they also serve who only sit and eat.

Most especially I want to thank Bill Zwicker and Cathy Brodie, David and Doris Cohen, Cutberto and Yolanda Garza, John and Matt Thorne, Carolyn Cox and Sam Perkins, Steve Spitz and Cynthia Ingols, Marjorie Senechal and Stan Sherer, Ron and Del Blank, Klaus Peters, Vickie Kearn, a generation of students, and Henles Allison, Fred, Portia, and Theda.

At the finish line I have been buoyed by the care, understanding, and enthusiasm of the staff at Princeton University PressDimitri Karetnikov, Carole Schwager, Mark Bellis, and though I mentioned her already, Vickie Kearn.

Some of the material in this book has been adapted from the Mathematical Intelligencer and permission has been granted by Springer Verlag.

Finally, the illustrations by Leon Steinmetz are quite amazing.

Jim Henle

July 2014

THE PROOF AND THE PUDDING

THE MAD SCIENTIST

WERE GOING to start with two investigations, one in mathematics and one in cooking. On the surface, they have little in common. There are similarities, though, similarities of spirit, for want of a better word. Ill say more at the end.

DOODLES

A few years ago, I was doodling, that is, I was sitting with pen and paper, drawing lines with no purpose in mind. I drew a square with grid lines.

I put diagonals in some of the boxes.

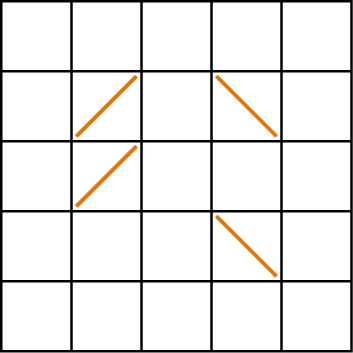
I imagined the lines as mirrors. I wondered what would happen if a ray of light entered the square and started bouncing around.

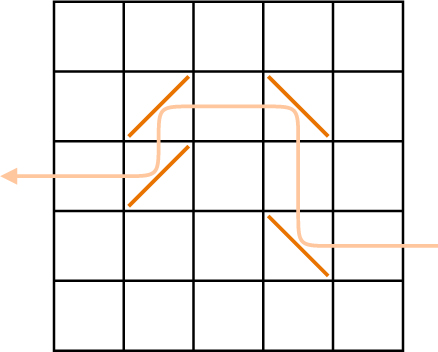
I noticed that it was possible for a ray of light to visit the same box twice, that is, it could bounce twice off the same mirror.

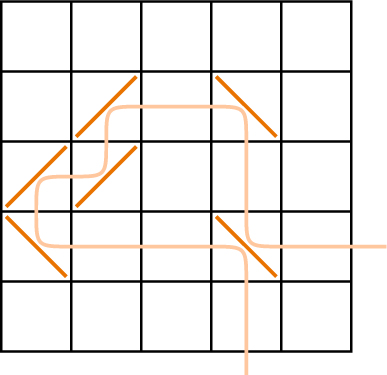
That made me wonder how long I could keep things going. Given a square, how long a path could I make, assuming I could place the mirrors wherever I wanted?

I started small. The 2 2 square allowed a path of length 5.

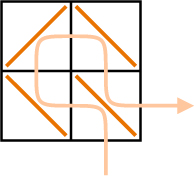
(I count each square I enter. I count a square twice if I enter it twice.)